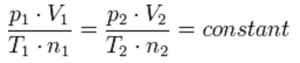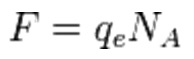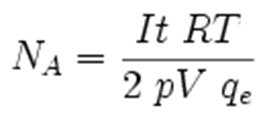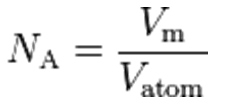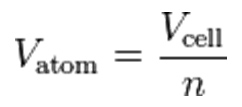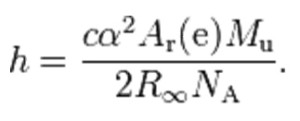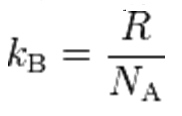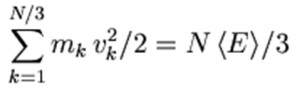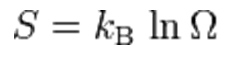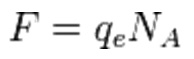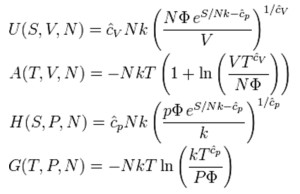Numero di Avogadro – Definizione

Porta il nome del suo scopritore italiano, il piemontese Amedeo Avogadro, il numero che costituisce il fattore di scala tra il mondo macroscopico – quello per intenderci che misura le cose sulla scala dei grammi – e quello a livello atomico e molecolare.

Un numero che, pur non costituendo secondo le definizioni correnti, una vera costante fisica, risulta di fatto comparire in una quantità sorprendentemente diversa di relazioni chimiche e fisiche, dimostrando in ogni caso un elevato valore esplicativo di inestimabile valore pratico ed anche didattico.

In realtà il sig. Avogadro non concepì in prima battuta un valore numerico.
Egli si limitò ad ipotizzare, negli anni compresi fra il 1809 ed il 1811 durante il suo insegnamento presso il collegio di Vercelli, che due campioni di quello che i fisici ancora oggi sono soliti chiamare un “gas ideale” o gas perfetto, nelle medesime condizioni di temperatura, pressione e volume, contengono lo stesso numero di molecole.  Il fatto di parlare di gas ideale pone certamente delle forti limitazioni che ci portano a discostarci di una certa misura dalle condizioni riscontrabili nella maggior parte delle esperienze pratiche, tuttavia questa limitazione non intacca minimamente il fatto che la sua identità chimica può essere delle più disparate, e di conseguenza la sua sezione molecolare/atomica e la sua massa molare.
In altre parole Avogadro aveva suggerito come il numero di molecole (o di atomi nel caso di una specie chimica monoatomica) nei due suddetti campioni di gas ideale, fosse sempre lo stesso, indipendentemente dalla specifica identità chimica del gas utilizzato, purché ovviamente soddisfacesse sempre alle caratteristiche di un gas ideale.
L’affermazione aveva tutte le caratteristiche per costituire una sorta di piccola rivoluzione nel mondo della chimica, in quanto consentiva – come illustreremo più avanti – di superare finalmente la barriera concettuale e di calcolo tra il mondo macroscopico, quello delle quantità pesabili ed osservabili delle sostanze chimica, e quello microscopico, ovvero dei singoli atomi e molecole, in sé stessi non manipolabili né soggetti ad un computo diretto ma sui quali si basano una grande quantità di leggi e di valutazioni scientifiche.

Purtroppo però il pensiero di Avogadro, pur pubblicato in una prestigiosa rivista scientifica dell’epoca (Journal de Physique, de Chimie et d’Histoire naturelle) rimase a lungo ai margini del dibattito scientifico dell’epoca: destino non migliore toccò anche al collega francese A. M. Ampére, che arrivò a conclusioni del tutto analoghe, pur seguendo un percorso dimostrativo diverso.
Formalizzata in seguito sotto forma di Legge di Avogadro, questa ipotesi si inquadra e completa tutto quel corollario di leggi (Gay-Lussac, Charles, Boyle-Mariotte) alle quali hanno contribuito tra fine ‘700 ed inizio ‘800 alcuni fra i più noti esponenti del pensiero scientifico del tempo e che, sempre per la solita idealizzazione del gas ideale, mettono fra loro in relazione temperatura, pressione, volume… e grazie ad Avogadro anche numero di molecole in un campione di gas.
Grazie a questo completamento del quadro è stato possibile pervenire a quella che oggi è comunemente definita come “legge dei gas” (perfetti) o equazione di stato dei gas, espressa dalla celeberrima formula pV=nRT, grazia alla quale note 4 delle 5 variabili in gioco per un dato campione di gas ideale è possibile calcolare matematicamente quella rimanente.
La Legge di Avogadro, in particolare, dimostra come il rapporto tra volume e “quantità di sostanza” (numero di molecole oppure numero di moli) della sostanza, a parità di temperatura e pressione, sia sempre costante

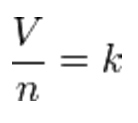
Ad esempio al crescere nel numero n di molecole, se non vogliamo che crescano proporzionalmente la pressione e/o la temperatura nel campione considerato (ricordiamo che avevamo detto che dovevano restare costanti) dovrà crescere il volume.

Con un minimo di calcolo matematico si arriva a stimare il valore della costante che non soltanto mette in relazione volume con quantità di sostanza, bensì tutti quanti i fattori che compaiono nell’equazione di stato dei gas perfetti: p, V, T, n.

Si tratta per la precisione della costante R, a questo punto giustamente denominata “costante universale dei gas”. Essa può assumere diverse unità di misura a seconda delle unità di misura adottate, oltre che per p, V e T, anche per il parametro n.

Nell’equazione precedentemente riportata, 1 e 2 si posso riferire sia allo stesso tipo di gas in condizioni differenti che a gas differenti in condizioni analoghe, o addirittura di gas chimicamente diversi, in condizioni di p, V, T ed n differenti, purché si rientri all’interno di quello che si sul definire un gas perfetto.

Nota.
Quello di gas perfetto è a tutti gli effetti soltanto un’idealizzazione teorica, che trova una certa approssimazione da parte dei gas reali soltanto in condizioni di ridottissima pressione ed altissima temperatura (in caso contrario si parla di “gas reali” ma l’equazione di stato inizia a complicarsi notevolmente).  Le quattro proprietà alle quali dovrebbe rispondere un gas perfetto sono
le molecole sono puntiformi;
interagiscono tra loro e con le pareti del recipiente mediante urti perfettamente elastici (ovvero non vi è dispersione di energia durante gli urti);
non esistono forze di interazione a distanza tra le molecole del gas: le molecole si dicono non interagenti;
le molecole del gas sono identiche tra loro e indistinguibili.

STORIA, STIME E MISURE DELLA COSTANTE DI AVOGADRO

La stima dapprima, e successivamente il calcolo esatto del valore del numero di Avogadro prende le mosse 54 anni più tardi rispetto all’intuizione di Avogadro, nella sperimentazione condotta da J.J. Loschmidt per valutare il numero di densità n0 di particelle contenute in un dato volume di gas ideale alla temperatura dello zero assoluto.

Fu poi il fisico francese Jean Perrin a proporre, nel 1909, di dedicare alla memoria del “numero” alla figura di Amedeo Avogadro, che per primo ne ipotizzò l’esistenza, quasi un secolo prima.  D’altra parte lo stesso Perrin doveva sentire una sorta di debito morale nei confronti del chimico piemontese, avendo legato buona parte del suo lavoro di scienziato alla determinazione del valore numerico di questa costante attraverso una molteplicità di metodi fra loro differenti, lavoro questo che gli valse il conseguimento del Premio Nobel per la chimica nel 1926.
Il passaggio formale da numero a “costante” (N_A) avvenne con ulteriore distanza di tempo, nel 1971, quando il Sistema Internazionale delle Unità (SI) decise di adottare la mole come unità di base per esprimere la quantità di sostanza, indipendentemente dalla dimensione della misura. In funzione di questa ridefinizione del concetto di mole, il numero (ora “costante”) di Avogadro cessò di essere un numero adimensionale, per acquistare l’unità di misura di un reciproco di mole (mol-1), in quanto rappresentava il numero di atomi contenuti in una mole di generica sostanza.
La determinazione “esatta” (o per meglio dire “accurata”) del valore del numero di Avogadro richiedeva tuttavia la possibilità di poter mettere in rapporto fra loro, utilizzando la stessa unità di misura, due dati indipendenti relativi rispettivamente alla scala microscopica (es. numero di molecole) e macroscopica (es. numero di moli) per la stessa specie chimica.  Questo è stato possibile solo nel 1910 ad opera del fisico americano Robert Millikan, che giunse ad una determinazione accurata del numero di Avogadro ricorrendo all’estensione della sua validità anche per le cariche elettriche, riassunta dall’espressione

Dove q_e è la carica elettrica di un singolo elettrone, mentre F è la costante già nota fin da 1834 come “costante di Faraday”, che misura la carica elettrica di una mole di elettroni, quantità facilmente ricavabile durante lo studio quantiativo dei processi di elettrolisi.
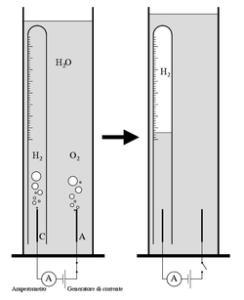
Attualmente fra i metodi di più comune utilizzo per la determinazione a fini didattici del numero di Avogadro vi sono quello elettrochimico: l’elettrolisi a pressione e temperatura costanti dell’acqua, fornisce un volume misurabile di idrogeno gassoso H₂ prodotto, insieme ad una certa quantità di carica (Q) transitata nel circuito, frutto questa del prodotto tra l’intensità di corrente (I) ed il tempo di erogazione (t).
L’espressione finale dalla quale si può ricavare il numero di Avogadro è:

Metodi più moderni ed accurati del numero di Avogadro si basano invece su considerazioni di natura cristallografica, quindi riferite allo stato solido di una specie chimica monoatomica. Tramite difrattometria a raggi X è possibile determinare la lunghezza di una singola cella cristallina: questo valore di tipo spaziale, insieme alla conoscenza della massa atomica relativa, consente di calcolare il numero di Avogadro alla stregua di una densità di materia nel cristallo medesimo, come è stato realizzato dal National Institute of Standard and Technology (NIST) su un cristallo di silicio, la cui geometria cubica consente – fra l’altro – di semplificare ulteriormente il calcolo

Dove V_m è il volume molare e V_atom il volume atomico della singola cella cubica, contenente un numero pari ad n=8 atomi di silicio.

La miglior stima ufficiale finora ottenuta per il numero di Avogadro è probabilmente:   6.02214129(27)×10²³ mol⁻¹

All’interno di un più ampio progetto scientifico internazionale volto ad eliminare il più possibile tutti i riferimenti a unità di misura “campione” di riferimento – e l’ultima di esse risulta ancora ad oggi essere il chilogrammo campione (gelosamente custodito a Sevres, in Francia) ha preso piede negli ultimi anni un progetto internazionale noto come International Avogadro Coordination, o più familiarmente “Avogadro project”.
Oggetto dell’esame è ancora una volta il silicio elementare, questa volta in forma di una sfera perfetta, avente massa appunto di 1 kg e composizione isotopica “naturale”.
La valutazione del numero di Avogadro dovrebbe emergere come conseguenza indiretta dal calcolo della costante di Plank

Lo studio tenderebbe a ripercorrere la fortunata esperienza che ha portato alla ridefinizione dell’unità di lunghezza in funzione non più di un “metro campione” bensì come prodotto di un tempo standard con una velocità costante (quella della luce, nota appunto come costante fisica fondamentale): nel caso della ridefinizione della massa si punterebbe su un’espressione del tipo N_Ah, nota come costante molare di Plank e ritenuta anch’essa una costante fisica fondamentale… forse più dello stesso numero di Avogadro di per sé, e strettamente legata al concetto stesso di massa.

Non che la cosa possa tornare di maggiore utilità pratica che non utilizzare direttamente il valore, già di per sé approssimato, di 6.22×10²³, ma si è notato che il numero di Avogadro è oggetto di una delle più note “coincidenze matematiche”, essendo approssimato con errore del solo 0.2% dalla 79esima potenza di 2, ovvero 2⁷⁹.

L’ANELLO DI CONGIUNZIONE FRA LA SCALA MACROSCOPICA E QUELLA MOLECOLARE

Il numero di Avogadro e, più in generale, la Legge che ne sottende l’esistenza formulata dallo scienziato piemontese, rappresenta l’ennesimo, ed uno dei più appariscenti, casi nei quali possiamo osservare una rassicurante convergenza di approcci, dimostrazioni e scuole di pensiero: dalla teoria cinetica dei gas alla cristallografia, dall’elettrochimica alla fisica quantistica. A riprova del fatto che il sapere scientifico – almeno così come oggi lo conosciamo – è continuamente alla ricerca di conferme, ed anche a fronte di un’ipotesi già ben confermata tanto sul piano sperimentale quanto su quello teorico, non si stanca di vagliare ulteriori riprove ed argomentazioni diverse.
Già a distanza di pochi anni dalla pubblicazione di Avogadro altri chimici e fisici del suo tempo evidenziarono risultati analoghi: oltre al già citato riscontro ad opera di Ampère, si ricordano R. Clausius con la sua teoria cinetica dei gas, J. H,, van’t Hoff con le sue ricerche riguardanti le soluzioni diluite, fino alle dimostrazioni sulle sostanze organiche allo stato gassoso ad opera di Gerhardt, Laurent e Williamson.

Il numero di Avogadro rientra anche nel calcolo di un’altra costante, probabilmente ancora più ricorrente in fisica, la costante di Boltzmann (kB o semplicemente k)

Dove R è ancora una volta la costante universale dei gas, già incontrata in precedenza. Il valore raccomandato dal CODATA per la costante di Boltzmann è:   1,3806488(24)x10^-23 K/K
Da notare in particolare come le unità di misura nelle quali si esprime kB siano le stesse utilizzate nel Sistema Internazionale per esprimere l’entropia e la capacità termica. Già questa semplice osservazione ci porta ad intuire, pur senza avere per il momento la capacità di esprimere con parole, qualcosa circa il “significato” profondo di questa costante.
La costante di Boltzamm ricorre in particolare quando si vogliono prendere in considerazione le caratteristiche dinamiche ed in particolare quelle termodinamiche di un sistema microscopico composto da particelle, ovvero quando le molecole (o gli atomi nel caso di specie chimiche monoatomiche) si comportano come unità distinte l’una dall’altra.
L’energia cinetica complessiva di un sistema del genere, composto di un numero N di molecole, per esempio è

Se vi state domandando dove mai compaia la costante di Boltzmann in questa equazione, significa che avete già dimenticato come essa sia in relazione con il numero di Avogadro e questo con il numero di molecole contenute in un campione di massa nota. Nella pratica questa doppia relazione ci consente, almeno in linea di principio, di affrontare una valutazione in termini particellari utilizzando come dati originali quelli di una semplice pesata di laboratorio.

La costante di Boltzam compare per esempio anche nell’equazione ritenuta “l’idea centrale” della meccanica statistica: quella che relazione i dettagli microscopici del sistema (Ω: il numero di microstati coerenti con le condizioni al contorno del sistema) con il suo stato macroscopico

Un’altra relazione fisica di grande interesse nella quale compare il numero di Avogadro è la già citata espressione di primaria importanza in campo elettrochimico, che mette in relazione la costante di Faraday (F) con la carica elettrica elementare dell’elettrone (qe): in questo caso è intuibile il ruolo di NA nella “transizione di scala” da una carica elementare, alla costante F che rappresenta quindi la carica elettrica portata da una mole di elettroni.

In termodinamica statistica il numero di Avogadro (N) compare nelle equazioni che mettono fra loro in relazione tutti i principali fattori di stato coinvolti nella descrizione del sistema: l’energia interna del sistema (U), l’entalpia (H) e l’energia libera di Gibbs (G), l’entropia (S), l’energia libera di Helmholtz ed il potenziale chimico (µ).

 
FATTORE DI CONVERSIONE FRA IL PESO E LE MOLI

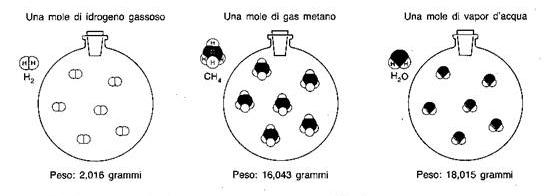
Una delle relazioni più note che coinvolgono il numero di Avogadro è quella secondo la quale esso corrisponde al numero di molecole di una certa sostanza contenute in una mole della stessa sostanza.
Dal momento che 1 mole è definita come la quantità di sostanza, espressa in grammi, pari al suo peso molecolare, ne deriva che il numero di Avogadro corrisponde al numero di molecole racchiuse in una quantità in grammi della sostanza descritta, numericamente uguale al valore del suo peso molecolare.

Facendo l’esempio dell’acqua, il cui peso molecolare – debitamente approssimato – è 18 u.m.a. (unità di massa atomica), una mole di questa sostanza corrisponderà al peso di 18 g; quindi 18 g di acqua conterranno un numero di molecole pari al numero di Avogadro.
Se la molecola è più grande (nel senso di costituita da un numero maggiore di atomi e/o da atomi “più pesanti”, cioè di peso atomico maggiore) aumenterà di conseguenza il suo peso molecolare, ma se pesiamo su una bilancia una quantità in grammi pari a questo suo peso molecolare, già sappiamo che in questa pesata ideale abbiamo messo insieme una numero di Avogadro di molecole di quella sostanza, ovvero 6.22E+23 molecole.
Tutto questo non si applica unicamente alle “molecole” propriamente dette ma può essere esteso senza alcuna difficoltà a tutte le specie chimiche, dai composti ionici quali ad esempio i sali, fino alle specie monoatomiche. L’unica differenza in questi casi consiste nella piccola formalità di dover sostituire la dicitura “peso molecolare” con quella, più corretta per queste specie, di peso formula o di peso atomico, a seconda dei casi.

Per quanto di primaria importanza in ambito scientifico e solitamente riportato in tutte le tabelle insieme alle più usate costanti chimiche e fisiche, il numero di Avogadro non può per definizione essere considerato come una “costante fondamentale”, come invece lo sono, per esempio, quella di Plank, quella di gravitazione universale, la carica dell’elettrone e la velocità della luce nel vuoto. La ragione di ciò risiede semplicemente nel fatto che il numero di Avogadro mette in relazione grandezze fisiche non omogenee ed arbitrarie, nel caso specifico il grammo (attualmente ancora riferito al kg campione, custodito a Sevres, in Francia) ed alla massa dell’isotopo 12 del carbonio.
Il riferimento al carbonio 12 è da intendersi in modo puramente formale, in quanto la definizione rigorosa del Numero di Avogadro lo descrive come “il numero di atomi dell’isotopo 12 del carbonio presenti in 12 grammi di tale sostanza”. Questa definizione non toglie comunque che lo stesso principio e lo stesso valore numerico si possano applicare, come descritto precedentemente, a qualsiasi altra specie chimica.

Quando si ha a che fare con numeri estremamente piccoli o, al contrario, estremamente grandi, non è mai facile farsi un’idea effettiva degli stessi di tipo diretta ed esperienziale, venendo a mancare ogni possibile riferimento con la nostra esperienza quotidiana. Ecco allora che si ricorre a metafore e visualizzazioni, basate su oggetti le sui dimensioni sono almeno in parte più “percepite”, se non a livello empirico, almeno su quello empatico. Wikipedia stessa ci fornisce alcuni spunti per aiutarci a visualizzare la vastità del numero di Avogadro, una cifra che, riportata per esteso e non in notazione scientifica – seppur con una certa approssimazione – può essere scritta come 602214129000000000000000:
“Se si prendesse un numero di palle da tennis pari a quello di Avogadro (quindi una “mole” di palle da tennis) e le si disponesse in modo omogeneo su tutta la superficie terrestre, si raggiungerebbe un’altezza di cinquanta chilometri, ovvero più di sei volte l’altezza del monte Everest. Ancora: se si disponessero tali palle in un’unica fila essa avrebbe una lunghezza pari a circa 20 128 000 000 chilometri, grosso modo 2 volte la larghezza di tutto il Sistema solare. Il numero di tazzine d’acqua contenute nell’Oceano Atlantico è dell’ordine di grandezza del numero di Avogadro, così come il numero di molecole d’acqua in una tazzina. Se la stessa quantità di centesimi di euro fosse distribuita uniformemente tra la popolazione mondiale, ogni abitante della Terra avrebbe mille miliardi di euro.”

CONSEGUENZE PRATICHE DEL NUMERO DI AVOGADRO

Utilizzando il numero di Avogadro possiamo calcolare il numero (virtualmente esatto) di molecole o di atomi contenuti in un dato campione di sostanza chimica. La condizione è che la sostanza sia chimicamente definita e pura e se ne conosca l’identità, ovvero di che sostanza esattamente si tratta.  Molti studenti rimangono meravigliati del fatto di sapere quante molecole siano racchiuse in un bicchiere d’acqua, in un cucchiaio di sale o in una bustina di zucchero.

I dati dei quali abbiamo bisogno per effettuare il calcolo sono il peso esatto del campione (ad esempio l’acqua nel bicchiere potrà pesare 95 g) ed il peso formula della sostanza. Con peso formula intendiamo la sommatoria dei pesi molecolari di tutti gli atomi che entrano a far parte della specie chimica che compone la sostanza in questione, indipendentemente dal fatto che si tratti di una sostanza molecolare (come l’acqua o il saccarosio) – per la quale possiamo tranquillamente parlare di peso molecolare – di una specie chimica monoatomica (per la quale avremo anche potuto usare il peso atomico) o infine di un composto ionico come ad esempio il cloruro di sodio. Nient’altro.

Tenendo ben presente il numero di Avogadro potremo calcolare con semplicità quanto occorre diluire una soluzione affinché – almeno dal punto di vista statistico – in un dato campione della soluzione vi sia presente un numero inferiore ad 1 unità (leggasi: molecola) del soluto. Detto in altri termini, un po’ meno precisi ma certamente più pittoreschi, si arriva in questo modo a calcolare quanto dobbiamo “allungare” una soluzione con il suo solvente affinché il soluto risulti di fatto assente.
Beninteso, non si tratta di scendere banalmente al di sotto dei limiti di sensibilità di indagine della strumentazione analitica, bensì di prendere consapevolezza del fatto che anche la materia – oltre all’energia – è una realtà quantizzata, e per tanto non può essere suddivisa infinitamente… o in questo caso diluita infinitamente.

Facciamo un esempio.  Se in 100 g di una soluzione acquosa, magari in una già molto molto diluita, abbiamo ancora 1000 molecole in soluzione (ad esempio molecole di glucosio), se prendiamo da questa un campione di 10 g e lo portiamo a 100 g con l’aggiunta di acqua pura (in pratica lo abbiamo diluito al 10% in peso) otterremo 100 g di soluzione contenente al suo interno 100 molecole di glucosio.
Se proseguiamo prendendo 10 g di questa seconda soluzione (contenenti al loro interno 10 molecole di glucosio) e li portiamo a 100 g con l’aggiunta di acqua pura, otterremo 100 g di soluzione contenente 10 molecole di glucosio.
Se prendiamo ancora 10 g di questa seconda soluzione (contenenti al loro interno 1 sola molecola di glucosio) e li portiamo a 100 g con l’aggiunta di acqua pura, otterremo 100 g di soluzione contenente 1 molecola di glucosio.
Se a questo punto prelevassimo nuovamente 10 g di questa soluzione, abbiamo solo una probabilità statistica su 10 che in essa riusciamo “a pescare” quell’unica molecola di glucosio che gira solitaria nella soluzione. Se volessimo ugualmente procedere in questo senso, magari suddividendo la soluzione in frazioni da 10 g ciascuna, da diluire ciascuna fino ai consueti 100 g con acqua pura, otterremo un set di 10 soluzioni acquose, delle quali ben 9 saranno di acqua assolutamente pura e solo una conterrà quella molecola di acqua che girava nella soluzione precedente.
Ovviamente anche nelle diluizioni precedenti la statistica si affacciava ad ogni passaggio: prelevando 10 g da 100 g di una soluzione contenente al suo interno 10 molecole non posso essere certo che 9 rimangano nei 90 g che non ho prelevato, e nel campione prelevato ne vada a finire uno soltanto. Mentre questa incertezza risulta del tutto trascurabile quando abbiamo a che fare con i numeri a decine di cifre che caratterizzano il contenuto di molecole dei campioni con i quali abbiamo solitamente a che fare, scendendo su scala delle diluizioni estreme la questione si fa più importante.

Torniamo dunque al numero di Avogadro.
Se prendiamo una quantità in grammi di glucosio puro pari al suo peso molecolare (in altri termini diremmo di avere preso “una mole” di glucosio), ovvero 180.16 e lo diluiamo con acqua fino ad 1 litro, questo litro di soluzione conterrà 1 mole di glucosio, quindi un numero di Avogadro di molecole di questa sostanza: 6.22×1023 molecole. Se preleviamo 1 ml di questa soluzione e la portiamo a volume di 1000 ml (ovvero 1 litro) con acqua pura, avremo abbassato la concentrazione di glucosio in questa soluzione di 3 ordini di grandezza: da 1M sarà diventata 0.001M, meglio rappresentabile come 1mM: prelevando 1 ml da questa soluzione, esso avrà solo 6.22×1020 molecole di glucosio al suo interno, ovvero 1/1000 della quantità contenuta in 1 ml della soluzione originale.  Continuando a diluire la soluzione secondo lo stesso criterio arriveremo a “quantità contenute” di 6.22×10¹⁷, 6.22×10¹⁴, ecc… 6.22×10², anche rappresentabile come 622 molecole di glucosio.  Se 1 ml di quest’ultima soluzione la porto a 622 g con acqua avrò ottenuto una soluzione avente dal punto di vista statistico 1 molecola di glucosio per ml. Ogni ulteriore diluizione, seguita da frazionamenti del volume di soluzione ottenuta, produrrebbe frazioni per la maggior parte completamente prive di molecole di glucosio.
Questa è solitamente una delle principali argomentazioni descritte per confutare le basi chimiche – o più in generale scientifiche – relative alla natura dei rimedi omeopatici usati in medicina, la cui diluizione nel più dei casi supera di fatto il limite di diluizione oltre il quale un campioncino rischia di risultare del tutto privo di molecole del principio attivo… o anche più semplicemente della pianta che viene descritta in etichetta del flacone.