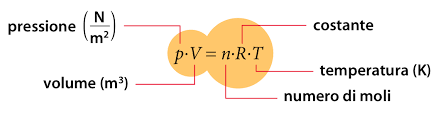Gas Ideale – Definizione e Significato

Tutti gli studenti si sono incontrati con la formula del gas ideale.

La bellezza di questa formula è che descrive il comportamento di tutti i gas.  Il prodotto della Pressione per il Volume è proporzionale al prodotto della Temperatura per il numero di moli n, attraverso la costante di proporzionalità R, la stessa per qualsiasi gas.
Però questa formula ha anche un grosso limite.  Non descrive esattamente il comportamento dei gas, ma solo in modo approssimato.  Se facciamo misure su di un certo gas, troviamo che il comportamento è circa quello previsto da P V = n R T, ma se le misure sono precise ci sono degli scostamenti.  E mentre la formula generale è la stessa per tutti i gas, questi scostamenti dipendono invece da quale gas consideriamo.

IL GAS IDEALE

Come interpretare questo stato di cose?  L’interpretazione corrente è che tutti i gas corrispondono a un modello di base che è lo stesso per tutti, ma poi ogni singolo gas se ne allontana con caratteristiche sue proprie. Si definisce allora il gas ideale, come quello che ha solo le proprietà generali e comuni a tutti. In altri termini, il gas ideale è, per definizione, quello che rispetta l’equazione P V = n R T.  Il gas ideale non esiste nella realtà, perché tutti i gas che veramente esistono, e detti per questo gas reali, si distaccano nel comportamento dal gas ideale.
A questo punto ci si può porre una questione: è veramente utile per la scienza definire qualcosa, come il gas ideale, che non esiste e non potrà mai esistere? Non sarebbe meglio studiare solo i singoli gas, con le loro differenze, e forse rimarcare le loro somiglianze, che non arrivano mai a diventare identità?
Sono convinto che il concetto di gas ideale, che è estesamente usato, sia molto utile per due ragioni, una pratica e una squisitamente teorica.  Quella pratica è che quasi sempre i gas reali si allontanano molto poco dal comportamento ideale, per cui l’equazione del gas ideale descrive le loro proprietà con buona approssimazione.  Questo è vero quando non si vanno a studiare i gas in condizioni estreme, come bassissime temperature o altissime pressioni, ma si devono maneggiare in situazioni che consideriamo normali, per esempio quando vogliamo misurare la quantità di un gas che si sviluppa in una reazione chimica.  In questi casi è uso comune utilizzare la formula del gas ideale, perché le differenze sono trascurabili sperimentalmente.  Il vantaggio è di usare una sola formula generale, ignorando del tutto di quale gas si tratti realmente.

Naturalmente un bravo sperimentatore dovrebbe sempre verificare, basandosi generalmente su dati di letteratura, che le deviazioni dall’idealità siano effettivamente trascurabili rispetto alla precisione delle sue misure. La ragione teorica è che il gas ideale occupa un posto importante nel quadro che ci facciamo della struttura della materia. Su questo torneremo più avanti.

Che cos’è una soluzione?
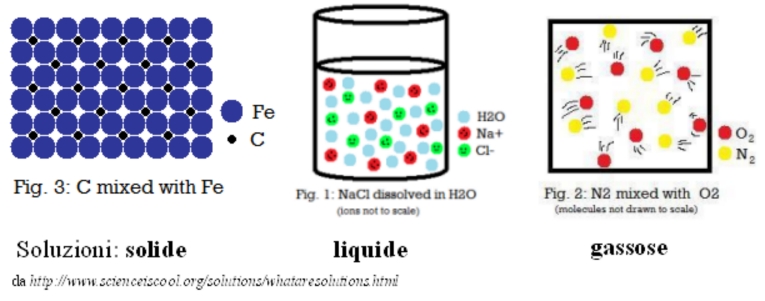
Anche per le soluzioni si parla di soluzione ideale.  Prima di procedere con la discussione, vorrei però fare una questione di linguaggio.  Se si parla rigorosamente, una soluzione è qualsiasi sistema omogeneo (cioè con proprietà uguali in tutti i suoi punti) formato da più di una sostanza.  Sono soluzioni, ad esempio, l’aria, che è formata di azoto, ossigeno e altri gas; l’acqua salata, formata di acqua e sale; il bronzo, formato di rame e stagno. Come si vede, le soluzioni possono essere solide, liquide o gassose.  Nel linguaggio corrente, però, il termine soluzione si usa soprattutto per le soluzioni liquide, e in particolare si pensa a un liquido puro di partenza, in cui si sia sciolta un’altra sostanza, che è chiamata soluto, mentre il liquido di partenza è detto solvente.  Per esempio, per fare l’acqua salata, immaginiamo di partire da acqua pura, che sarà il solvente, e scioglierci dentro del sale, generalmente in quantità relativamente piccola, che sarà il soluto.  E’ anche comune considerare soluzioni con più soluti sciolti in uno stesso solvente.  Il soluto allo stato puro può essere solido, come il sale, o liquido o gassoso, ma nella soluzione è allo stato liquido. Nel seguito parleremo di soluzioni intendendo solo le soluzioni liquide, in cui un componente, il solvente, è molto più abbondante del soluto o dei soluti.

La soluzione ideale
Per definire la soluzione ideale si usa di solito il concetto della tensione di vapore.  Questa è una grandezza propria di qualsiasi liquido, non solo delle soluzioni.  Vediamo di cosa si tratta. Qualsiasi liquido, se messo in un recipiente chiuso senza riempirlo, passa in parte allo stato gassoso, che in presenza del liquido si usa chiamare vapore.  Fra liquido e vapore si stabilisce un equilibrio dinamico, nel senso che parte del liquido continua sempre ad evaporare, passando allo stato gassoso, ma contemporaneamente parte del vapore passa allo stato liquido.  Questo porta ad uno stato in cui le quantità di liquido e di vapore presenti non cambiano più, anche se vapore e liquido si rinnovano continuamente.  Questo stato di equilibrio è caratterizzato da una ben determinata pressione del gas (vapore), che è detta tensione di vapore.  All’equilibrio questa pressione non cambia più nel tempo.  La descrizione precedente è nell’ipotesi che sopra il liquido ci sia, a parte il vapore, solo il vuoto.  Se, come comunemente avviene, c’è invece dell’aria, il quadro non cambia in maniera importante; bisogna solo notare che la pressione dell’aria viene ignorata e si considera solo la pressione del vapore.  L’equilibrio dipende in modo importante dalla temperatura: la tensione di vapore è costante a temperatura costante, ma aumenta con la temperatura.
Si definisce soluzione ideale una soluzione che rispetta la legge di Raoult:

p₁ = p_1⁰ n₁/(n₁+n₂)

Questa formula si riferisce a una soluzione formata da un solvente, che indichiamo con 1, e un soluto, che indichiamo con 2.  La soluzione è formata da n₁ moli di solvente e n₂ moli di soluto.   p₁⁰ è la tensione di vapore del solvente puro (quando non c’è il soluto), e p₁ è la tensione di vapore del solvente sulla soluzione.
La definizione di soluzione ideale può sembrare completamente diversa da quella di gas ideale, ma in realtà c’è una profonda somiglianza.  Elaborando matematicamente la formula della legge di Raoult, la si può mettere nella forma seguente:

Π V = n₂R T

Ora la somiglianza con la legge del gas ideale è evidente.  La costante R è la stessa del gas ideale, V è il volume della soluzione, e Π è una pressione, detta pressione osmotica.  Per capire il significato della pressione osmotica, consideriamo che in ogni soluzione i componenti (soluto e solvente) tendono a distribuirsi uniformemente in tutta la soluzione, e non ad accumularsi in regioni diverse.  Ora, se poniamo a contatto due soluzioni a concentrazione diversa, oppure una soluzione col solvente puro, abbiamo un sistema (complessivo) in cui il soluto è distribuito in maniera non uniforme.  Questo sistema non sarà in equilibrio stabile, ma passerà spontaneamente a uno a concentrazione uniforme, facendo passare del soluto dalla soluzione più concentrata a quella più diluita o al solvente puro, oppure del solvente dalla più diluita alla più concentrata.  Questa tendenza può essere rappresentata da una pressione, appunto la pressione osmotica, che spinge il solvente puro, a contatto con la soluzione, ad entrarvi dentro; nel caso di due soluzioni a contatto, il solvente passa spontaneamente dalla pressione osmotica minore a quella maggiore.  La pressione osmotica è un fatto sperimentale che si può misurare accuratamente, e ha particolare interesse negli organismi viventi, quando un liquido a concentrazione relativamente alta, per es. il sangue, viene a contatto con acqua pura o contenente poco soluto.
C’è una differenza importante fra la soluzione ideale e il gas ideale.  Né l’una né l’altro esistono nella realtà, ma mentre i gas reali rispettano abbastanza bene la legge ideale, nelle soluzioni reali abbiamo scostamenti importanti, che dipendono dalla particolare soluzione che consideriamo.  Tutte le soluzioni tendono al comportamento ideale quando sono molto diluite, ma mentre alcune mantengono un comportamento quasi ideale anche a concentrazioni alte, altre soluzioni mostrano presto deviazioni così importanti che è difficile riconoscere anche solo lo schema del comportamento ideale.  Per discutere le ragioni di questa differenza fra gas e soluzioni, è venuto il momento di parlare, teoricamente, di come si interpretano gas e soluzioni ideali in termini di struttura.

Modello del gas ideale
Secondo la legge del gas ideale il prodotto P V, per un dato gas a una certa temperatura, è proporzionale a n, il numero di moli di gas.  E’ quindi proporzionale a n anche il solo V se la pressione è costante, e la sola P se il volume è costante.  Per le soluzioni si può dire lo stesso del prodotto Π V.   Il numero di moli n è a sua volta proporzionale al numero di molecole N, in quanto ogni mole è, per definizione, un numero di Avogadro A = 6,02•10²³ di molecole:

N = n A

Quindi, per un gas, sia la pressione che il volume, quando il resto è costante, sono proporzionali al numero di molecole.   L’interpretazione più semplice di questo fatto è un modello del gas ideale in cui ogni molecola occupa un volume (se la pressione è costante) o esercita una pressione (se il volume è costante) che sono fissi, cioè dipendono solo dalla molecola stessa e non risentono della presenza o meno di altre molecole.   In altri termini, un modello in cui pressione e volume misurabili sono semplicemente la somma di pressioni e volumi molecolari; ancora in altri termini, in cui non esistono ulteriori proprietà dovute a interazioni fra le molecole.
Che i volumi siano additivi (cioè che mescolando due corpi si ottiene un volume finale che è la somma dei loro volumi) è esperienza comune.   Se verso due bottiglie da 1 L di acqua, riempio esattamente una bottiglia da 2 L.   Lo stesso con due bottiglie da 1 L di alcool.  Attenzione però: questo non è un effetto necessario e universale, ma richiede che le condizioni delle molecole non cambino col mescolamento.   Se infatti mescoliamo 1 L di acqua con 1 L di alcool, non otteniamo 2 L ma solo 1,92 L.   Questo si spiega considerando che ogni molecola di acqua prima era circondata solo da altre molecole di acqua, e dopo da molecole di acqua e di alcool; lo stesso per le molecole di alcool. Le molecole nella nuova condizione occupano ciascuna un volume leggermente minore di quello di prima.   Per i gas, se mescoliamo 1 L di un gas con 1 L di un gas anche diverso, otteniamo (se restano invariate temperatura e pressione) sempre 2 L. Questo ci suggerisce che nei gas ogni molecola non ha praticamente rapporti con le altre molecole, e quindi non è sensibile né al loro numero né alla loro qualità.
Venendo alla pressione, abbiamo bisogno innanzitutto di un modello che spieghi perché un gas esercita una pressione sulla parete del recipiente che lo contiene.   Il modello è quello di molecole in movimento continuo e disordinato, per cui la pressione, che è l’azione di una forza su di una superficie, è dovuta agli urti delle molecole sulle pareti del recipiente.   Quando una molecola urta una parete, rimbalza all’indietro senza scambiare energia, e questo richiede che eserciti una forza sulla parete, o, cosa equivalente, che la parete eserciti la stessa forza sulla molecola, forza che fa cambiare di direzione la sua velocità.  La somma di queste forze in un dato istante, diviso la superficie, è la pressione esercitata dal gas.
Prima di parlare dell’effetto delle molecole di gas l’una sull’altra, immaginiamo una situazione semplicissima (e non realizzabile praticamente, ma serve solo per la discussione): un recipiente rigido che contenga una sola molecola di gas.   Questa molecola, secondo il modello delineato prima, si muove con una velocità v in una direzione a caso.   La velocità sarà costante nel tempo: possiamo capirlo con considerazioni meccaniche, perché nessuna forza agisce sulla molecola; o con considerazioni energetiche, perché (detta m la massa della molecola) la sua energia cinetica E = ½mv² non deve variare.
La molecola si muoverà quindi in linea retta sempre con velocità v, ma non indefinitamente.  A un certo punto urterà una parete del recipiente e il suo moto cambierà, ma come?   Siccome abbiamo supposto che non scambi energia con la parete, la sua velocità cambierà di direzione ma non di modulo, in modo da lasciare invariata l’energia cinetica.   In termini più semplici, la molecola rimbalzerà semplicemente sulla parete come una palla.   Il numero di urti sarà proporzionale alla velocità della molecola (più la molecola è veloce, più presto arriva a urtare) e la forza esercitata nell’urto sarà proporzionale alla massa e ancora alla velocità della molecola (più la molecola è veloce, maggiore è la variazione della componente della velocità che deve invertire la direzione quando la molecola rimbalza).   La forza totale esercitata da tutti gli urti sarà in definitiva proporzionale al quadrato della velocità e alla massa, e quindi all’energia cinetica, che è appunto ½mv².   Questa forza, diviso la superficie, costituisce la pressione.   La descrizione è un po’ semplificata, perché le molecole possono urtare la parete in modi diversi: di fronte, esercitando una forza maggiore, o di striscio, esercitandone una minore; ma questo non è importante, perché nella realtà gli effetti si mediano.

Interazioni fra le molecole
Stabilito che una sola molecola che si muove a caso esercita una pressione, vediamo cosa succede se, come sempre avviene, le molecole sono molte.  Dobbiamo spiegare due aspetti della legge del gas ideale: che la pressione è proporzionale al numero di molecole, e che la costante di proporzionalità è la stessa per qualunque gas, nonostante le molecole di gas diversi abbiano massa diversa.
Consideriamo prima un gas che sia una sostanza pura, cioè formato di molecole tutte uguali.
L’ipotesi più semplice per giustificare il fatto che la pressione è proporzionale al numero di molecole, è che ogni molecola eserciti la sua pressione, col meccanismo descritto per una sola molecola, come se le altre non ci fossero, o come se si trovasse da sola nel recipiente.  Una difficoltà è che, avendo supposto che il moto delle molecole sia a caso, due molecole avranno di solito velocità diversa, e quindi energia cinetica diversa.  Poiché la pressione, come abbiamo visto, è proporzionale all’energia cinetica, le due molecole non eserciteranno la stessa pressione.  Considerando la pressione totale esercitata dal gas, questa sarà la somma dei contributi dalle singole molecole, ma il contributo non è lo stesso per ogni molecola: le molecole (per caso) più veloci contribuiscono più di quelle più lente.  E’ impossibile seguire la velocità di ogni molecola, ma per i nostri scopi basta considerare l’energia cinetica media < ½mv² > (usiamo il simbolo < > per indicare la media, su tutte le molecole, dell’espressione racchiusa fra le parentesi angolari).  Infatti, sebbene ogni molecola dia un contributo diverso, la pressione totale è la stessa che si avrebbe se ogni molecola desse un contributo uguale, dovuto all’energia media.
Ma torniamo all’ipotesi che ogni molecola si muove come se le altre non ci fossero.  Quanto è ragionevole questa ipotesi?  Significa che le molecole non si urtano, non si attraggono e non si respingono.  Ora, le molecole hanno una massa e sono fatte di particelle con carica elettrica.  Per la legge di gravità, le masse si attraggono; le cariche elettriche (anche se il loro totale è zero) si trovano su particelle positive e negative, e possono disporsi in modo da attrarsi o respingersi (con considerazioni più complicate, si può vedere che l’attrazione prevale leggermente sulla repulsione).  Se vogliamo mantenere l’ipotesi che ogni molecola è come se fosse sola, dobbiamo supporre che queste attrazioni non esistano nel gas ideale, e che nei gas reali, quando si comportano come quello ideale, siano così piccole da essere trascurabili.  Ora, le attrazioni gravitazionale e elettrostatica diminuiscono con la distanza, quindi l’ipotesi che non ci siano si può giustificare se le molecole si trovano a grande distanza l’una dall’altra.  Facciamo un veloce calcolo, considerando un litro di un gas a 0°C e a pressione atmosferica.  Esso contiene 2,69•10²² molecole, che disperse a caso si trovano a una distanza media di 3,3•10^-9 m l’una dall’altra.  La grandezza di ogni molecola dipende dal modo di definirla e da qual è il gas, ma per es. per l’ossigeno O₂ le dimensioni sono un po’ meno di 0,3•10^-9 m.  Si vede quindi che le molecole sono a distanza più di 10 volte maggiore del loro diametro; per fare un paragone, un uomo ha dimensioni dell’ordine di 1 m, ed è come se le persone riempissero una piazza, ma stando a distanza di più di 10 m l’una dall’altra.
Risulta essere ragionevole quindi pensare che le molecole siano così lontane che attrazioni e repulsioni non esistono (nel gas ideale) o sono trascurabili (in un gas che ha comportamento quasi ideale). Ma c’è ancora un effetto che non possiamo trascurare: gli urti.   Anche se le molecole sono mediamente lontane, il loro moto casuale le porterà ogni tanto vicine fino ad urtarsi. Nell’urto il loro moto cambierà di velocità e direzione; non possiamo rappresentarci una singola molecola come se si muovesse sempre diritta facendo ping-pong fra una parete e quella opposta; il suo moto sarà uniforme solo fra un urto e l’altro, e la traiettoria complessiva sarà uno zig-zag, in cui ogni segmento avrà anche una velocità diversa.  Ma questo non cambia in modo importante il quadro che ci siamo fatti prima.  Basta supporre che negli urti le molecole non cambino la loro struttura interna e quindi la loro energia, a parte l’energia cinetica.  Per esprimere questo con una parola, gli urti devono essere elastici.  Allora, per la legge di conservazione dell’energia, in ogni urto cambierà la velocità e l’energia cinetica delle molecole che si urtano, ma non l’energia cinetica totale.  E poiché la pressione dipende solo dall’energia cinetica media, possiamo concludere che gli urti fra le molecole non hanno effetto sulla pressione che esse esercitano.

Molecole non uguali
Il modello deve ancora spiegare perché, cambiando il gas o considerando una miscela di gas diversi, la pressione P e il volume V non cambiano, ma dipendono semplicemente dal numero totale di molecole, senza distinguere di che tipo sono.  Abbiamo visto che la pressione totale dipende solo dal n. di molecole e da < ½mv² >, la loro energia cinetica media.  Dobbiamo allora ipotizzare che molecole diverse, che hanno massa diversa, hanno la stessa energia cinetica media.   Questo significa che molecole più pesanti (con massa maggiore) devono avere velocità media minore, per avere la stessa energia cinetica.  Con parole più semplici, il modello richiede che le molecole più pesanti si muovano più lentamente.  E’ una previsione verificabile e confermata sperimentalmente.

La temperatura
Consideriamo ora la temperatura. L’equazione P V = n R T prevede che la pressione, il volume o il loro prodotto siano direttamente proporzionali alla temperatura.   Ma abbiamo già visto che il modello prevede che essi siano proporzionali all’energia cinetica media.   La conclusione necessaria è che la temperatura è una misura dell’energia cinetica media < ½mv² > delle molecole.   La temperatura, quella che si misura con un termometro, perde così il suo aspetto misterioso, che in passato si è tentato di legare a un fluido (il calore?) che passa da un corpo all’altro, e diventa una grandezza fisica interpretabile in termini di meccanica e di moto.  Questa interpretazione richiede anche che esista uno zero assoluto della temperatura, in quanto la velocità delle molecole può diminuire al massimo fino a fermarle completamente. Anche questa previsione è confermata, e lo zero assoluto si trova a T = 0 K = -273,15°C.
Riassumiamo il modello del gas ideale. E’ costituito da un gran numero di molecole che si muovono a caso, in uno spazio molto grande rispetto alle loro dimensioni.  Le molecole si urtano con urti elastici e percorrono traiettorie a zig-zag.  Quando le molecole urtano le pareti del recipiente, rimbalzano esercitando una pressione, con un effetto proporzionale all’energia cinetica media.  Molecole grandi o piccole hanno lo stesso effetto, perché un aumento della massa è bilanciato da una diminuzione della velocità media.  La temperatura è la misura dell’energia cinetica media.

Le soluzioni
Per le soluzioni la situazione è più complicata, e fare un modello della soluzione ideale è più difficile.  Per tentare di spiegare perché la tensione di vapore è costante, conviene usare un modello cinetico, cioè ragionare sulla velocità dell’evaporazione, che conduce all’equilibrio fra il liquido e il vapore.
Le molecole di un liquido si attraggono fortemente l’un l’altra, e questo le tiene vicine in uno spazio limitato, fino alla superficie del liquido.  Al di sopra della superficie non c’è liquido.  Le molecole vicino alla superficie, muovendosi a caso, possono passare nello spazio sovrastante, dove si troveranno allo stato gassoso.  Il passaggio richiede un consumo di energia, e avverrà a spese dell’energia della molecola nel liquido, che come abbiamo visto per i gas è misurata dalla temperatura.  Avremo così un’evaporazione continua, con una velocità che dipende fortemente dalla temperatura, ma è costante ad una data temperatura.  Le molecole di gas, a loro volta, possono attraversare la superficie e ritornare nel liquido, ma la velocità di questo passaggio, anche a temperatura fissa, non è costante ma proporzionale al numero di molecole e quindi, per la legge dei gas, alla pressione.  Il sistema va all’equilibrio quando la velocità di riassorbimento è uguale alla velocità di evaporazione, e quindi a una pressione costante, che è la tensione di vapore.
Quanto sopra per un liquido puro.  Perché in una soluzione ideale la tensione di vapore del solvente diminuisce?  Facciamo un modello in cui la singola molecola di solvente nella soluzione si trova nella stessa situazione che nel solvente puro, e ha la stessa tendenza a evaporare.  Allora la differenza fra solvente puro e soluzione è che, nella soluzione, non tutte le molecole in superficie sono di solvente, ma solo una frazione n₁/(n₁+n₂).  La velocità di evaporazione diminuirà quindi di questo fattore, e anche la velocità di riassorbimento dovrà diminuire dello stesso fattore per uguagliarla.  E poiché questa velocità è proporzionale alla pressione del vapore, la pressione di equilibrio, cioè la tensione di vapore del solvente sulla soluzione, diminuirà dello stesso fattore, come espresso dalla legge di Raoult

p₁ = p₁⁰ n₁/(n₁+n₂)

Il modello della soluzione ideale si fonda sull’idea che le singole molecole di solvente si comportino come se le altre molecole (di soluto) non ci fossero, e le proprietà della soluzione dipendano solo dal numero delle molecole di solvente.  Questo è analogo al modello del gas ideale, dove ogni molecola di gas si comporta come se le altre molecole di gas non ci fossero, e le proprietà del gas dipendono solo dal numero delle molecole.

Gas e soluzioni ideali, ma non solo
Ritorniamo alla domanda iniziale: a che serve introdurre questi concetti ideali? La risposta è che essi non servono a studiare la realtà nei suoi svariati dettagli, ma servono per aiutarci a farci un quadro ordinato dei fenomeni che osserviamo.  Facendoci modelli semplificati, del gas con molecole assolutamente indipendenti, delle soluzioni con molecole di solvente che non cambiano di proprietà rispetto al solvente puro, noi riusciamo a prevedere e descrivere vari comportamenti anche abbastanza complessi, che proprio per la semplicità del modello devono essere generali e non specifici per un particolare sistema che studiamo.  Così, quando consideriamo poi un particolare sistema, non siamo costretti a indagare e spiegare il suo comportamento generale, ma solo le deviazioni dal comportamento ideale.

I gas reali corrispondono piuttosto bene al gas ideale, perché l’ipotesi (ideale) che le molecole siano assolutamente indipendenti si verifica facilmente se le molecole reali sono molto lontane l’una dall’altra.  Nelle soluzioni liquide, invece, le interazioni intermolecolari sono sempre importanti, come del resto nei liquidi puri; è quindi più difficile che in una soluzione le singole molecole di solvente non risentano della presenza del soluto, e questo giustifica le maggiori deviazioni dal comportamento ideale.
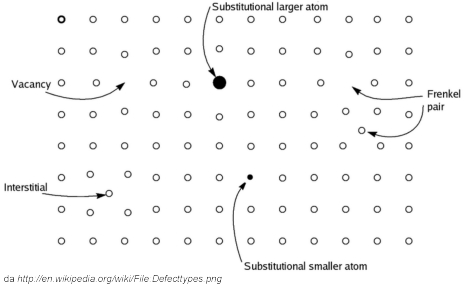
Il concetto di un sistema ideale è così utile che viene introdotto anche in altri campi.  Per esempio, si può definire un solido ideale.  Nei solidi cristallini le particelle costituenti (atomi, molecole o ioni) si dispongono ordinatamente nelle tre dimensioni dello spazio.  Possiamo definire ideale un solido che abbia quest’ordine perfetto.  In un solido reale, inevitabilmente, l’ordine non viene sempre rispettato rigorosamente, e abbiamo la possibilità di particelle in più, o in meno, o spostate, o diverse.  Questi sono complessivamente chiamati difetti. In un solido reale le proprietà dipendono in parte dalla struttura ideale, perfettamente ordinata, e in parte dai difetti.

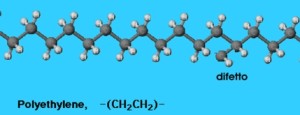
Un altro esempio è quello dei polimeri. Un polimero è una molecola a catena formata dalla ripetizione in sequenza di una stessa struttura chimica.  Anche in un polimero troviamo i difetti, come irregolarità nella sequenza.  Il polimero senza difetti è un polimero ideale, e le proprietà di un polimero reale (plastica, fibra) dipendono dal polimero ideale corrispondente e dai difetti.

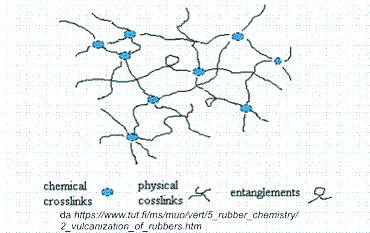
Anche per la gomma si può definire una gomma ideale.  La gomma è formata da catene polimeriche che hanno inizio e termine su nodi da cui partono altre catene, formando una struttura complessiva come una grande rete.  L’estrema deformabilità della gomma si spiega con una capacità delle catene di scorrere l’una rispetto all’altra senza alcun impedimento, ma col vincolo che la struttura generale della rete deve restare invariata.  La gomma ideale è descritta dalla struttura a rete e dall’assoluta libertà di movimento dei tratti di catena.  Una gomma reale non è ideale perché le catene, anche se scorrono facilmente, non sono però assolutamente libere, e perché la struttura non è perfettamente a rete, per es. ci sono tratti di catena che terminano liberi invece di finire su un nodo.
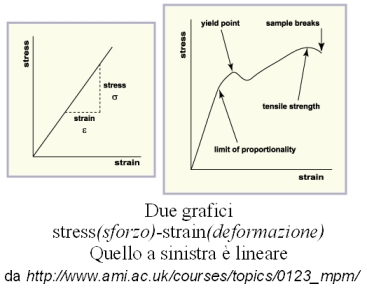
Le tecniche discusse hanno in comune l’idea di base, quella di immaginare prima un sistema più semplice, quindi più facilmente comprensibile e descrivibile, e introdurre poi le complicazioni quando se ne presenti la necessità. Questo si fa spesso anche in assenza di un modello fisico, usando solo la matematica. Se una certa grandezza fisica A cresce al crescere di un’altra grandezza B, si può fare una prima descrizione supponendo che A e B siano proporzionali fra di loro, salvo rivedere poi quest’ipotesi e introdurre dipendenze più complesse.  Questa tecnica si chiama di linearizzazione, perché una proporzionalità diretta si vede in un grafico come una linea retta.

Un esempio è nello studio delle proprietà elastiche dei materiali.  Quando si applica una forza, il materiale si deforma tanto più quanto maggiore è la forza.  Allora si suppone che la deformazione sia proporzionale alla forza applicata, e il rapporto fisso fra i due si chiama modulo elastico, un’importante proprietà di un materiale.  Se poi si guarda bene il grafico forza-deformazione, si vede che una proporzionalità diretta non spiega il grafico, se non nel tratto iniziale di piccole forze e deformazioni.  Più avanti i punti misurati non si allineano lungo una retta. Nella scienza dei materiali, occorre allora procedere per spiegare la non-linearità.
In elettricità, quando si applica una differenza di potenziale agli estremi di un conduttore, si produce una corrente elettrica che è proporzionale al potenziale (legge di Ohm). Mentre questa legge spiega e permette di progettare il comportamento di importanti apparati elettrici, come elettrodotti e motori, essa è insufficiente per descrivere i dispositivi elettronici, oggi così importanti: per questi occorrono considerazioni molto più complicate.

Per concludere, lo studente deve realizzare che molti degli insegnamenti che riceve, nei più vari campi della scienza, non riflettono la realtà in tutti i dettagli che siamo in grado di conoscere, ma sono degli strumenti utili per semplificare questa realtà e permettergli di inquadrarla, rimandando ad approfondimenti successivi la discussione delle differenze tra i modelli semplificati e l’evidenza sperimentale.