Indice
Nella chimica, come nelle altre scienze di base, lo scopo fondamentale è l’analisi e la comprensione descrittiva dei fenomeni al fine di individuare delle leggi generali in grado di fare delle previsioni. La base fondamentale del metodo scientifico risiede, quindi, nell’osservazione del fenomeno, nella sua ripetibilità e conseguente misurabilità. Un fenomeno casuale, ovvero non ripetibile, non è misurabile. Come conseguenza, non è possibile trarre per esso delle leggi previsionali.
Ci sono diversi motivi per cui un fenomeno può essere casuale. Tra questi grande importanza hanno gli errori nelle misure sperimentali oppure il fatto che il fenomeno sia avvenuto senza il controllo delle condizioni al contorno, cioè si sia verificato un cambiamento nelle condizioni sperimentali durante l’esecuzione dell’esperimento. Un esempio potrebbe essere una variazione di temperatura, pressione o altro di cui non ci si è accorti.
Da quanto argomentato, il metodo scientifico si basa sulla misura sperimentale che a sua volta si basa sull’interpretazione dei numeri che sono come l’alfabeto per una lingua: senza di esso non è possibile costruire né le parole né tantomeno le frasi per affrontare un discorso di senso compiuto.
Lo scopo di questi appunti è quello di fornire i primi rudimenti del linguaggio matematico usato per l’interpretazione dei risultati sperimentali con particolare attenzione ai bisogni della chimica. In particolare, questi appunti sono un utile riferimento per gli studenti del primo e secondo anno delle ex Facoltà di Agraria che si avvicinano allo studio della chimica generale e della chimica del suolo. Con queste note, non si intende assolutamente sostituire i normali corsi di analisi matematica indispensabili per acquisire sia il linguaggio che la mentalità scientifica. Piuttosto si desidera fare in modo che alla fine della lettura di questi appunti, lo studente abbia compreso come leggere un numero dopo aver effettuato una misura sperimentale.
NOTAZIONE SCIENTIFICA
Con l’affermazione dei moderni elaboratori elettronici l’uso della notazione scientifica o esponenziale è ormai diventata familiare ai più. Essa consiste nello scrivere i numeri sotto forma di potenze intere di 10, ovvero si deve distinguere un coefficiente (un numero compreso tra 1 e 9) ed un esponenziale (il 10 elevato a potenza) che viene indicato anche come ordine di grandezza del numero in esame. Questa notazione è necessaria in campo scientifico perché consente di evitare di manipolare numeri o troppo grandi o troppo piccoli il cui uso disturba la lettura ed appesantisce i calcoli. Un esempio è la carica elettrica di un elettrone che corrisponde a 0.00000000000000000016 Coulomb o la distanza percorsa dalla luce in un anno che corrisponde a 9460000000000000 metri.
Ricordando che 101 = 10, 102 = 10 x 10, etc e che 10-1 = 1/10 = 0.1, 10-2 = 1/102 = 1/(10 x 10) = 0.01 etc. si può scrivere come esempio di notazione scientifica:
2500=2.5 x 103; 150000=1.5 x 105; 10=1 x 10; 0.1=1 x10-1; 0.001=1 x 10-3; 0.0000524=5.24 x 10-5; 0.00000000000000000016=1.6 x 10-19; 9460000000000000=9.46 x 1015.
Nell’esempio appena letto, i diversi numeri sono di ordini di grandezza differenti. Per esempio tra 2.5 x 103 e 1.5 x 105 ci sono due ordini di grandezza di differenza mentre tra 1.6 x 10-19 e 9.46 x 1015 ci sono ben 49 ordini di grandezza di differenza. L’ordine di grandezza del primo numero (2.5 x 103) è delle migliaia (103), quello del secondo numero (1.5 x 105) delle centinaia di migliaia (105). La differenza tra gli esponenti è proprio la differenza tra gli ordini di grandezza.
Si noti che la notazione usata per il raggruppamento delle cifre e per la separazione dei decimali è quella anglosassone in cui il “.” (punto) viene usato al posto della “,” (virgola) dal momento che l’Inglese è il linguaggio scientifico oggi riconosciuto per la divulgazione delle informazioni.
Le operazioni con i numeri esponenziali si effettuano ricordando che esse vanno effettuate sia sui coefficienti che sugli esponenziali.
Esempio 1:
(2.3 x 10-1) x (1.2 x 10-5) = (2.3 x 1.2) x (10-1 x 10-5) = 2.76 x 10-6
(2.3 x 10-1) / (1.2 x 10-5) = (2.3 / 1.2) x (10-1 / 10-5) = 1.916 x 10-4
(2.3 x 10-1) + (1.2 x 10-1) = (2.3 + 1.2) x 10-1 = 3.5 x 10-1
(2.3 x 10-1) + (1.2 x 10-2) = (2.3 x 10-1) + ( 0.12 x 10-1) = 2.42 x 10-1
(2.3 x 10-1) – (1.2 x 10-2) = (2.3 x 10-1) – ( 0.12 x 10-1) = 2.18 x 10-1
Si noti come per la somma e la differenza, i numeri sono stati resi confrontabili trasformando gli esponenziali in modo tale da mostrare la stessa potenza.
LE UNITA’ DI MISURA. I MULTIPLI ED I SOTTOMULTIPLI
Come evidenziato nel paragrafo precedente, l’uso della notazione scientifica è fondamentale quando si devono esprimere le misure di grandezze fisiche.
Una grandezza fisica è una qualsiasi proprietà di un sistema che può essere suscettibile di misura. Per esempio, l’altezza di un tavolo, ovvero la distanza tra il pavimento e la sua superficie, è una grandezza fisica dal momento che può essere misurata.
Fare una misura di una grandezza fisica vuol dire confrontare tale grandezza con una analoga usata come riferimento. Affinché due grandezze possano essere confrontate esse devono essere consistenti, ovvero una lunghezza va confrontata con una lunghezza, una superficie con una superficie, un volume con un volume etc etc.
La misura si esprime moltiplicando un numero per una unità dimensionale. Le unità dimensionali associate alle grandezze fisiche sono definite nel sistema internazionale (SI) come in Tabella 1.
Alla luce di quanto appena riportato, dire che l’altezza di un tavolo è di 1 m significa che la distanza tra il pavimento e la superficie del tavolo è pari a quella tra le due estremità di una sbarra che viene presa come riferimento ed indicata come “metro” (la definizione corretta di metro è quella che lo considera come la distanza percorsa dalla luce nel vuoto in un intervallo di tempo pari a 1/299792458 di secondo). Si rimanda ai testi di fisica per la definizione corretta delle varie unità di misura elencate nella tabella precedente.
La dimensione di una grandezza fisica può essere sia una frazione che un multiplo delle unità elencate in Tabella 1. Qui di seguito i multipli e sottomultipli delle unità SI in notazione scientifica.
Tabella 2. Multipli e sottomultipli delle unità di misura in notazione scientifica.
| Sottomultipli | Multipli | ||||
| fattore | nome | simbolo | fattore | nome | simbolo |
| 10-1 | deci | d | 10 | deca | da |
| 10-2 | centi | c | 102 | etto | h |
| 10-3 | milli | m | 103 | chilo | k |
| 10-6 | micro | m | 106 | mega | M |
| 10-9 | nano | n | 109 | giga | G |
| 10-12 | pico | p | 1012 | tera | T |
| 10-15 | femto | f | 1015 | peta | P |
| 10-18 | atto | a | 1018 | exa | E |
Sulla base delle Tabelle 1 e 2, una distanza pari ad 1 mm corrisponde a 10-3 m ovvero alla millesima parte del metro. Allo stesso modo una distanza di 1 m corrisponde alla milionesima parte del metro.
COSA SIGNIFICA FARE UNA MISURA SPERIMENTALE
Come evidenziato nel primo paragrafo, affinché un fenomeno possa essere studiato è necessario che esso sia ripetibile, ovvero che si ripeta sempre nello stesso modo ogni qual volta esso viene studiato. Studiare un fenomeno significa individuare una grandezza fisica associata al fenomeno ed effettuarne delle misure quantitative. La variazione nelle misure consente di determinare la legge generale in grado di descrivere il fenomeno. A titolo di esempio si consideri la seguente reazione chimica che descrive la formazione della ruggine:
3Fe + 4H2O → Fe3O4 + 4H2↑
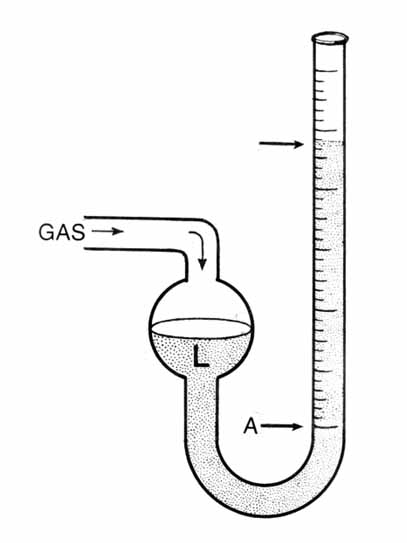
Se si intende studiare la velocità con cui si forma la ruggine è necessario innanzitutto individuare una qualsiasi grandezza che consenta di descrivere la reazione. La grandezza che si può prendere in considerazione è la quantità di idrogeno (H2) gassoso che si forma e che varia nel tempo. Si misura la pressione di idrogeno che si evolve a 1 minuto, 2 minuti, 10 minuti, 30 minuti etc dall’inizio della reazione. Una volta raccolti i dati sperimentali si disegna un grafico dal quale si ottiene la legge cinetica attraverso processi di interpolazione grafica. Per lo studio dettagliato della cinetica si rimanda alla lezione apposita. Ciò che si intende evidenziare qui è il processo di misura che consiste nel valutare il cambiamento della pressione di idrogeno man mano che la reazione evolve. La pressione può essere misurata con un manometro. Cambiando manometro, il risultato non cambia. Ciò che può cambiare è il numero di cifre con cui la pressione misurata viene espressa.
I NUMERI NELLE MISURE SPERIMENTALI
Il modo di maneggiare i numeri nelle scienze sperimentali è molto diverso da quello della matematica. Per esempio la √(2) è un numero che si può esprimere come 1.4142135623730950488016… In pratica da un punto di vista matematico si possono scrivere infinite cifre per la radice quadrata di 2. Allo stesso modo il rapporto 1/3 si esprime matematicamente come 0.3333333….., ovvero uno 0 seguito da infiniti 3.
Da un punto di vista sperimentale, esprimere la misura di una grandezza con un numero infinito di cifre non ha alcun senso.
Supponiamo di fare una pesata usando diversi tipi di bilance. Una bilancia misura un peso di 1 g, una seconda un peso di 1.0 g, una terza un peso di 0.99 g ed una quarta 0.988 g.
Riassumendo:
pesata 1: 1 g
pesata 2: 1.0 g
pesata 3: 0.99 g
pesata 4: 0.988 g
Che differenza c’è tra le diverse pesate?
La prima bilancia pesa con l’approssimazione del grammo. La seconda bilancia approssima al decimo di grammo, la terza al centesimo di grammo e l’ultima approssima la pesata al millesimo di grammo. Cosa significa approssimazione al grammo, decimo di grammo, centesimo di grammo o millesimo di grammo? Significa semplicemente che la bilancia è uno strumento che consente di misurare il peso di un corpo con un certo margine di errore dovuto alla lettura della scala della bilancia.
La figura mostra due scale con due livelli di accuratezza differenti. La freccia a sinistra indica un punto della scala che è vicino ad 1. Tuttavia, dal momento che fra 0.5 ed 1 non c’è gradazione, non è possibile stabilire con accuratezza quanto il valore letto si discosti da 1. La freccia a destra, al contrario, indica un punto su una scala con una suddivisione in intervalli più piccoli. Per questo motivo è possibile leggere che il valore della misura (il peso) non è 1.0, ma 0.9.
In altre parole, la scala a sinistra consente di leggere il valore della misura per intervalli di 0.5 unità, mentre la scala a destra consente di leggere per intervalli di 0.1 unità. Aumentando la suddivisione della scala è possibile aumentare il grado di accuratezza della misura. Da quanto descritto, si capisce che il limite sul numero di cifre con cui esprimere una misura dipende da quanto accurata è la scala strumentale. Come conseguenza, non è possibile esprimere il valore di una misura con un numero di cifre infinito.