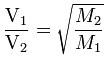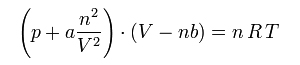Indice
Quello gassoso costituisce uno degli stati di aggregazione fondamentali – il più semplice – della materia, almeno di quella materia poco meno che esotica che siamo soliti immaginare organizzata in atomi.
Esattamente come per gli altri stati di aggregazione della materia (liquido e solido) anche un gas può essere composto da singoli atomi – ovvero da specie chimiche monoatomiche come per esempio i gas nobili – oppure da più atomi legati fra loro da un legame chimico, ovvero da molecole. In questo secondo caso possiamo avere molecole omoatomiche, composte da due o più atomi dello stesso elemento legati fra loro (es. N2) oppure da atomi di elementi diversi come nel caso dell’anidride carbonica.
Spesso si fa una certa confusione tra i concetti di gas e di vapore, utilizzando questi termini un po’ come sinonimi l’uno dell’altro. In verità entrambe le condizioni di esistenza della materia – comunemente definita “aeriforme” sono accomunate dal fatto che entrambi tendono ad occupare virtualmente “tutto” il volume nel quale sono confinati, adattando la distanza e quindi la rarefazione spaziale tra le particelle in funzione dell’entità di questo volume.
Una distinzione tra gas e vapore della stessa sostanza può essere effettuata sia su base teorica che sperimentale. Per definizione, una sostanza di tipo aeriforme è considerata gas quando esso si trova ad una temperatura superiore a quella nota come “temperatura critica”, mentre è considerato vapore quando si trova ad una temperatura inferiore a questa.
Da un punto di vista sperimentale, un gas non è condensabile, cioè non può essere portato allo stato liquido comprimendolo a temperatura costante (si ricorda, per inciso, che per compressione un gas tenderebbe ad aumentare la sua temperatura). Al contrario, un vapore diventa liquido quando è sufficientemente compresso a temperatura costante. Empiricamente, quando una sostanza inizia a liberarsi allo stato aeriforme dalla corrispondente fase liquida – ad esempio in seguito a riscaldamento – o anche per sublimazione, quello che si sviluppa sarà senz’altro un vapore. Solo a temperature nettamente superiori la stessa sostanza potrà trovarsi allo stato di gas.
A titolo di esempio, l’acqua a pressione ambientale sarà in condizioni di vapore dai 100°C ai 374°C circa (che corrisponde alla temperatura critica di questa sostanza), mentre si comporterà come gas a temperature superiori a quest’ultima, fino alla sua eventuale decomposizione.
COSIDERAZIONI ESTERIORI SUI GAS
Dal punto di vista del comportamento, osservabile anche esteriormente, una sostanza allo stato gassoso di differenzia rispetto alla stessa sostanza in un altro stato di aggregazione (es. liquido o solido) per via della tendenza manifestata dal gas ad occupare virtualmente tutto lo spazio disponibile. Va da sé che come i liquidi, anche i gas assumeranno la forma del contenitore nel quale sono posti.
Un gas mostra una tendenza macroscopica a “spostarsi”, o meglio ad espandersi in tutte le direzioni, ben maggiore di quella di un liquido e, a differenza di questo, sembrerebbero almeno in apparenza immuni alla forza di gravità, tanto che se togliamo il tappo da un contenitore pieno di gas appoggiato su di un tavolo in una stanza, dopo un po’ di tempo il gas si sarà diluito in tutto il volume del locale, dal pavimento al soffitto. In realtà sappiamo che la stessa aria risulta costituita da gas, precisamente da una miscela gassosa composta prevalentemente dalla molecola biatomica di azoto, seguita in ordine di concentrazione da quella biatomica di ossigeno: di conseguenza il fatto che un gas possa espandersi liberamente in modo uniforme e con la stessa velocità verso l’altro e verso il basso è fortemente determinata dalla sua densità relativa (peso per unità di volume) nei confronti dell’aria. Da qui il fatto che l’elio e l’idrogeno tendono a salire rispetto all’azoto dell’aria, mentre gas “pesanti” come ad esempio il monossido di azoto e tanti altri che caratterizzano l’atmosfera urbana inquinata dal traffico stradale, tendono a ristagnare verso il basso. In una stanza dove venisse praticato il vuoto, ovvero dove l’aria risultasse assente, un palloncino riempito di elio ed uno riempito di aria tenderebbero entrambe ad adagiarsi al suolo.
DESCRIZIONE CINETICA E DESCRIZIONE TERMODINAMICA
Lo studio, descrizione e la previsione del comportamento dei gas può essere affrontato dalla fisica secondo diversi approcci e punti di vista, tutt’altro che in contraddizione fra loro, che da un punto di vista della “filosofia della conoscenza” rappresentano semplicemente un’espressione del fatto che l’uomo può accedere alle verità oggettive della natura non in modo diretto, bensì solo attraverso rappresentazioni ideali di forme e di dinamiche. I nostri organi di senso creano nella nostra consapevolezza alcuni tipi di rappresentazioni degli oggetti e dei fenomeni, mentre la stessa descrizione matematica consente di maturarne altri. L’importante è che le conclusioni e quindi anche le previsioni (confermabili sperimentalmente) che i diversi tipi di approccio non risultino in contraddizione fra loro.
E’ questo il caso dell’approccio di tipo cinetico rispetto a quello di tipo termodinamico nella descrizione del comportamento dei gas, tanto di quello ideale quanto di quelli reali.
La teoria cinetica dei gas parte dalla rappresentazione di un gas alla stregua di un insieme di particelle molto piccole, caratterizzate da un movimento costante e casuale che le porta ad urtarsi reciprocamente e ad urtare le pareti del contenitore nel quale il gas è contenuto. Uno dei fattori chiave di questa visione sta nella descrizione della pressione del gas unicamente come un effetto dell’urto delle particelle contro le pareti del contenitore (uno stesso misuratore di pressione contrappone sempre una sorta di “parete” sensibile che limita l’espansione del gas, assorbendone gli urti delle particelle), senza tenere conto dei fenomeni di attrazione o – ancor più rilevanti – di repulsione “statica” (ovvero indipendente dal fatto che esse siano provviste di moto) tra una particella e l’altra.
Pur partendo da alcune “ipotesi” che, detto in verità, risultano applicabili solo in casi limite, ovvero nel cosiddetto caso del “gas ideale”, la teoria cinetica dei gas arriva a descrivere in modo attendibile il rapporto esistente tra pressione, volume, temperatura e numero di particelle contenute nel campione di gas, con un’attendibilità che dipende direttamente da quanto le ipotesi iniziali delle teoria vengono rispettate dal caso reale nel quale esse si collocano.
L’approccio termodinamico alla fisica dei gas parte in primo luogo a considerare il gas stesso come un corpo unitario, soggetto alle leggi della termodinamica ed ai suoi parametri di descrizione, proprio ad iniziare da quelli inerenti i trasferimenti di calore da e verso l’ambiente esterno (da cui il nome stesso di termodinamica) e dalle sue funzioni di stato come l’energia interna, l’entalpia e l’entropia, per terminare con l’espressione di grandezze di grande riscontro concreto come la capacità termica ed il calore specifico.
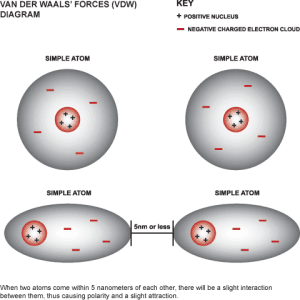
Altri possibili punti di approccio per la descrizione del comportamento osservabile nei gas possono a ragione essere quello relativo ai cosiddetti “moti browniani” (incentrati sulle ragioni e sulle conseguenze dei moti particellari spontanei) ed allo studio delle interazioni esistenti fra le singole particelle di gas, espresse a loro volta da forze intermolecolari quali quelle descritte da Van der Waals e da London.
PROPRIETA’ DEI GAS
Le argomentazioni scientifiche relative alle proprietà ed alle caratteristiche dei gas, accumulate e man mano dimostrate a partire dal XVIII secolo, sono talmente tante, incisive e coerenti fra loro da far sì che quello gassoso rappresenti a tutti gli effetti tra quelli che la materia può assumere lo stato più proficuamente indagabile, ovvero quello dove le leggi della fisica e della chimica tendono a semplificarsi, o meglio ancora ad avvicinarsi quasi asintoticamente ad una loro formulazione ideale.
Tra le numerosissime e talvolta peculiari proprietà e parametri per mezzo dei quali possiamo descrivere un dato gas, a parte quelle di natura propriamente chimica (specie chimica e numero di moli), ricordiamo:
Pressione
Volume
Temperatura critica
Velocità di effusione
Vicinanza al comportamento del “gas ideale”
La temperatura critica di un gas rappresenta la temperatura al di sopra della quale non è più possibile effettuare una transizione di stato da gas a liquido per semplice aumento della pressione, come invece avviene per i vapori.
Nei paragrafi successivi avremo modo di illustrare meglio il significato fisico e l’estrapolazione matematica del valore numerico della temperatura critica per un dato gas.
La velocità di effusione è un parametro di caratterizzazione tipico degli aeriformi, in quando a differenza del normale spostamento della massa di un liquido o di un solido nel suo insieme, tale da rispondere alle leggi della meccanica ed in particolare della dinamica, si riferisce alla naturale tendenza da parte di un aeriforme di occupare, seppur non istantaneamente, l’intero volume del contenitore ermetico nel quale esso è posto. A differenza di un solido o di un liquido che si muove sotto l’effetto di una forza esterna (banalmente anche la semplice forza di gravità) senza la quale resterebbe immobile, le particelle di gas si muovono, finendo con l’allontanarsi l’un l’altra, sulla spinta dei moti browniani.
Come osservò il chimico scozzese Thomas Graham (1805-1869), da cui l’omonima legge dei gas, ragionando per coppie di gas chimicamente puri e differenziati proprio per la natura chimica delle molecole o degli atomi che li compongono, è possibile mettere in rapporto la velocità di effusione di un gas rispetto all’altro, con la radice quadrata di una massa molare rispetto all’altra.
GAS IDEALE
Partendo dal presupposto che l’idealità per essere tale non può trovare un riscontro effettivo nel nostro mondo, possiamo riassumere in tre semplici punti le caratteristiche che vorremmo attribuire ad un ipotetico gas per poterlo definire ideale:
– Le singole particelle (atomi o molecole che siano) hanno natura puntiforme, ovvero sono così infinitamente piccole da poter essere considerate adimensionali;
– Allo stesso modo le singole particelle possono essere considerate prive di massa, e quindi di peso;
– Le singole particelle non interagiscono fra loro in nessun modo, né interagiscono con le eventuali pareti del contenitore nel quale il gas è posto.
Per quanto si tratti semplicemente di un modello ideale, per certi versi non molto diverso da una figura platonica dal sapore un po’ filosofico, l’astrazione all’idealità ha consentito storicamente, e consente ancora oggi specie sul piano didattico, di comprendere meglio alcune fondamentali proprietà e leggi di comportamento dello stato gassoso, leggi e comportamenti che potranno poi, seppur con una certa approssimazione, essere riversate anche sui gas non proprio ideali, ovvero i cosiddetti gas reali.
Un gas reale può quindi avvicinarsi di più o di meno al comportamento del gas ideale (tendenza all’idealità), dando di conseguenza la possibilità di studiarne e prevederne il comportamento secondo le equazioni semplificate sviluppare per il caso del gas ideale. In generale il comportamento sarò tanto più ideale quanto più il gas si trova ad una temperatura elevata (rispetto al suo punto di ebollizione) ed in uno stato di rarefazione, ovvero a pressione ridotta. Per quanto riguarda la temperatura, convenzionalmente si ritiene di poter assimilare il comportamento di un gas reale a quello di un gas ideale quando la sua temperatura supera di almeno un ordine di grandezza (ovvero di un fattore di almeno x10 volte) la sua temperatura critica.
E’ a questo punto facile immaginare come il comportamento di un vapore non possa essere descritto con una sufficiente attendibilità facendo riferimento al gas ideale.
EQUAZIONE DI STATO
Pressione, volume, temperatura ed infine il numero di “entità” chimiche separate (es. molecole) che caratterizzano una porzione di gas isolato, sia esso inteso come ideale oppure come reale, sono quattro grandezze strettamente correlate fra loro, tanto che non se ne può far variare una senza che almeno un’altra vari anch’essa di conseguenza.
A partire dalla fine del XVIII secolo furono diversi i fisici europei che descrissero, tramite le leggi che oggi prendono il loro nome, specifici comportamenti dei gas in relazione alla variazione di parametri fisici quali la temperatura, la pressione, il volume a disposizione ed infine anche – unico parametro che si potrebbe definire “chimico” – il numero di moli della sostanza gassosa.
I fisici Gay-Luccac, Charles e Volta, quasi contemporaneamente seppur con sperimentazioni diverse, dimostrarono che, a pressione costante, il volume di un gas aumenta linearmente con la temperatura. Si tratta un po’ dell’effetto della mongolfiera, che non si gonfia perché è in pressione (infatti è ampiamente aperta verso il basso) ma grazie al fatto che l’aria o in generale la miscela gassosa soffiata dentro ad essa è a temperatura sensibilmente più alta di quella dell’ambiente esterno al pallone.
I fisici Boyle e Mariotte osservarono, anch’essi quasi simultaneamente, qualcosa che oggi ci appare ancora più familiare: quando comprimiamo un gas in uno spazio chiuso, riducendone in volume, ovviamente operando a temperatura costante, la pressione del gas aumenta (vedi video).

E’ il caso delle pompe volumetriche, come ad esempio quelle che utilizziamo per gonfiare le ruote della bicicletta: dal momento che il cilindro con pistone della pompa è collegato alla camera d’aria della bicicletta, quando imprimiamo forza sul pistone delle pompa il volume complessivo a disposizione gas diminuisce (l’aria viene “spostata” tutta nel solo pneumatico) e la sua pressione di conseguenza cresce.
Allo stesso modo se proviamo a tappare con un dito una siringa di plastica (senza ago!) mentre spingiamo sul pistoncino per rimuoverne l’aria, sentiremo una pressione che cresce proporzionalmente a quanto avremo ridotto il volume della siringa a sua disposizione.
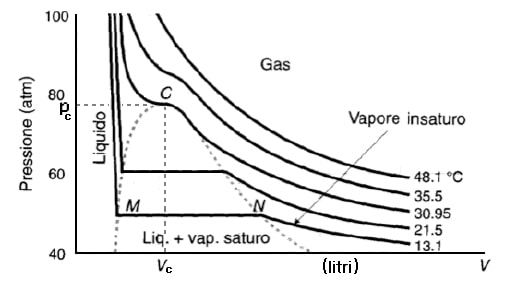
Rappresentando graficamente questa legge su un piano che ha per assi cartesiano appunto la pressione ed il volume (diagramma noto anche come “piano di Calpeyron”), ogni esperimento condotto ad una temperatura costante diversa può essere rappresentato sotto forma di una curva continua: il grafico qui riportato per esempio mostra l’andamento dei valori di pressione e di volume del gas per 5 esperimenti, condotti rispettivamente a 48,1°C, 35,5°C, 30,95°C, 21,5°C e 13,1°C. A partire dalla terza curva (30,95°C) e sempre più per temperature inferiori, si assiste ad un’anomalia nella curva della temperatura, che sembra attraversare una regione piatta, ovvero di invarianza, nella quale viene a mancare la relazione p*V=costante descritta in precedenza: questa è in effetti la zona del diagramma di Andrews nella quale la combinazione dei valori di temperatura, pressione e volume sono tali da consentire la liquefazione del gas. La temperatura limite per l’instaurarsi di questo importante fenomeno (in grafico visualizzata al punto C) è nota come temperatura critica.
Infine ancora i fisici Gay-Lussac e Volta notarono che se vincoliamo come costante il volume di un gas (ad es. in un contenitore con le pareti rigide) la sua pressione cresce linearmente con la temperatura. E’ il motivo per cui se mettiamo a scaldare una bomboletta che contiene un gas, anche non infiammabile quindi anche semplicemente aria, rischiamo di provocarne l’esplosione, o per lo meno la rottura.
Espressa in modo matematico, questa legge si può riassumere come: p*V=costante
Dalla quale si comprende facilmente che, per mantenere il valore costante del prodotto, qualsiasi esso sia, un aumento della pressione deve corrispondere ad un’equivalente riduzione del volume, e viceversa.
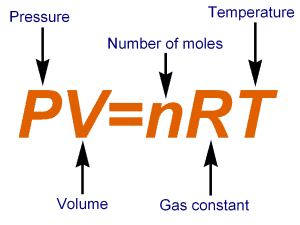
Tutte queste descrizioni di effetti, pur sempre singolarmente validissime, sono infine state riunite in un’unica legge, che prende il nome di Legge dei Gas Perfetti, rappresentata dalla celeberrima equazione: pV=nRT
In questa equazione compaiono due termini moltiplicativi che non figuravano in modo esplicito nelle tre leggi “parziali” precedentemente sviluppate: n ed R.
“n” è sicuramente il legame più forte tra la fisica dei gas e la loro natura chimica, in quanto è costituito dal numero di moli della specie chimica gassosa contenute nel sistema gassoso esaminato. Estraendo n dall’equazione di stato dei gas ideali si ottiene:
n = (pV)/(RT) che ci offre la possibilità di calcolare quante moli di gas sono contenute nel nostro sistema conoscendo solo i valori di pressione di volume e di temperatura, o addirittura il peso molecolare del gas (ammesso che si tratti di una specie chimica pura e che questa rispetti sufficientemente le condizioni di idealità) conoscendo il peso del gas introdotto.
R non costituisce invece un fattore da misurare nei singoli esperimenti, bensì una costante di proporzionalità, che assume valori numerici differenti a seconda delle unità di misura adottate per gli altri tre parametri (p, V, T), mentre n è sempre espresso come numero di moli. Essa prende il nome di “costante universale dei gas”, o semplicemente di “costante dei gas”.
Quando il volume è espresso in litri (L), la pressione in atmosfere (atm) e la temperatura in gradi Kelvin (K), essa assume il valore di 0,0820784. Nel caso più raccomandabile in base alle convenzioni internazionali, ovvero con il prodotto pressione*volume espresso nel suo insieme in Joule (J) e la temperatura in gradi Kelvin (K), la costante R assume il valore di 8,314472.
Si può facilmente realizzare un esperimento utilizzando un gas in condizioni non troppo dissimili da quelle ideali, dove previa la misurazione dei valori di p, V, T ed n è possibile stimare sperimentalmente il valore della costante R dei gas.
Il fatto di essere riusciti a concepire un’equazione unica per descrivere il comportamento del gas ideale ci consente infine di svincolarci da quelle piccole clausole che caratterizzavano tutte e tre le leggi precedentemente esposte, ovvero quella di Boyle-Mariotte e le due di Volta-Gay-Lussac: il fatto che la loro validità individuale fosse condizionata dall’invarianza di uno dei fattori in gioco, ovvero la pressione quando si facevano variare il volume e la temperatura, il volume quando si facevano variare la pressione e la temperatura, ed infine la temperatura quando si facevano variare la pressione ed il volume.
Quando ci apprestiamo a misurare sperimentalmente i fattori che entrano in gioco nell’equazione del gas ideale riusciamo a toccare con mano quello che, circa un secolo più tardi e, lo so, in un contesto del tutto diverso, Heisenberg arrivò a teorizzare circa l’influenza esercitata dall’atto stesso di “misurare” sull’entità della grandezza misurata.
Se misuriamo una temperatura con un termometro, non possiamo ignorare che il fenomeno fisico che ci consente di trasformare la temperatura in qualcos’altro di visibile ad occhio, assorbe esso stesso calore. Dall’innalzamento della colonnina di mercurio per dilatazione termica dello stesso ad una termocoppia, fino ad arrivare alle transizioni di stato per i critalli liquidi, la misurazione termometria stessa, quasi per definizione, assorbe calore. Lo stesso dicasi per la pressione: tutti gli strumento utilizzati per la misura della pressione hanno in fondo una cosa in comune: oppongono a questa pressione la pressione di una loro parte, solitamente mobile, sia essa ancora una volta una colonna di liquido, con il suo peso, oppure una parete deformabile.
Per il volume il discorso sembrerebbe diverso, ma solo in apparenza. Certo non dobbiamo immaginare un gas racchiuso in un contenitore dalla pareti rigide ed indeformabili, ovvero a volume costante, ma una condizione più simile a quella di una bolla di sapone, o al limite di un palloncino. Sappiamo infatti che un gas, spontaneamente, tenderebbe ad espandersi indefinitamente, fino ad occupare un volume teoricamente infinito. Dal momento che un gas è limitato nello spazio, questa è comunque da considerare una condizione di costrizione imposta dall’esterno, misurabile indipendentemente dalla sperimentazione sul gas. Riguardo al volume, la sperimentazione sul gas ideale comporta una condizione quasi per definizione irrealizzabile nella pratica sperimentale: quello di un contenitore che limiti la libera ed infinita espansione del gas, ma che al tempo stesso risulti liberamente deformabile, e quindi ampliabile nel volume, qualora il gas tendesse ad un’espansione motivata da ragioni termodinamiche più forti, come ad esempio da un aumento di temperatura oppure da una riduzione della pressione.
La maggioranza degli strumenti utilizzati per la misurazione della pressione, dal vecchio manometro a mercurio ai più moderni controller digitali, condividono il fatto di necessitare al loro interno di una membrana deformabile (ed il segnale letto dallo sperimentatore è infatti proprio proporzionale al grado di deformazione) in relazione alle condizioni differenziali di pressione tra la faccia della membrana rivolta verso il gas da valutare e quella rivolta verso l’ambiente esterno, o nei più moderni dei casi da sistemi piezoelettrici che, in un modo o nell’altro, assorbono anch’essi una parte del lavoro della pressione nell’atto stesso di misurarla.
Forse forse l’unico fattore dell’equazione dei gas ideali che non risulta influenzato dalla misurazione stessa è rappresentato proprio dal numero di moli (n) della specie chimica interessata.
I GAS REALI
Talvolta piuttosto simili al modello ideale del gas perfetto, in altri casi fortemente discosti da questo, fino al caso estremo dei vapori, i gas e le loro miscele con i quali abbiamo a che fare tanto nella vita reale quanto in laboratorio, sono molecole – o più raramente atomi isolati – dotati sì di una loro massa, per quanto molto piccola, ed anche di un loro volume molecolare. Le singole unità (es. molecole) di questi gas reali possono interagire fra loro in una molteplicità di modi diversi, sia in occasione di urti casuali tra le particelle che interagendo a distanza, oltre a poter interagire con le pareti del contenitore che li racchiude.
Anche se sono stati proposti modelli più raffinati, un’estensione della legge dei gas perfetti in direzione della “realtà” dei gas ordinari è rappresentata dalla Legge di van der Waals (datata 1873 a firma del fisico olandese Johannes Diderik van del Waals)
Alla pressione è addizionato un termine a *n2/V2 che tiene conto delle interazioni reciproche di tipo attrattivo fra le unità molecolari (o atomiche) di gas: al diminuire del volume ovviamente questo fattore di interazione cresce perché le particelle, così ravvicinate, hanno una maggiore probabilità di attrarsi fra loro e quindi di urtarsi reciprocamente. Questa attrazione fra le molecole riduce, seppur di poco, la frequenza e l’energia degli urti delle stesse molecole con le pareti del contenitore, parametro che siamo soliti misurare come indicazione della pressione del gas al suo interno. La pressione teorica, quella che consentirebbe di gestire l’equazione alla stregua di quella per i gas ideali, prevede quindi che alla pressione misurata si debba addizionare matematicamente questo contributo a*n2/V2 che potremo in qualche modo considerare come una sorta di pressione dissipata internamente.
Ci si potrebbe domandare a questo punto per quale ragione un gruppo di molecole, tutte identiche fra loro, si dovrebbero attirare reciprocamente: perché gli urti che abbiamo descritto sono solo in minima parte casuali, essendo in larga parte il risultato di un’attrazione fra le molecole. Si tratta per lo più di attrazioni tra dipoli elettrici formati dalla distribuzione asimmetrica delle cariche elettriche sulla superficie delle molecole.
Al contrario, il fattore nb viene sottratto al volume complessivo occupato dal gas in quanto trattasi del volume realmente occupato dall’insieme delle singole particelle: si ricorderà infatti che gran parte del volume occupato da un gas è in realtà volume vuoto, all’interno del quale gli atomi o le molecole si muovono, urtano reciprocamente e contro le pareti del contenitore, e solo una piccola parte di questo volume risulta occupato dalle particelle medesime. Pur non completamente e/o non costantemente occupato dalla materia della quale sono costituiti gli atomi e le molecole del gas, questo volume di pertinenenza di ciascuna particella microscopica di gas esercita tramite la sua nuvola elettronica un effetto repulsivo sulle altre unità di gas presenti nello stesso ambiente.
Man mano che ci si discosta dal caso del gas ideale, il volume realmente occupato dalle singole particelle aumenta rispetto al volume complessivo del gas e bisogna quindi sottrarlo da questo per garantire il rispetto dell’equivalenza termodinamica fra p*V ed n*R*T.
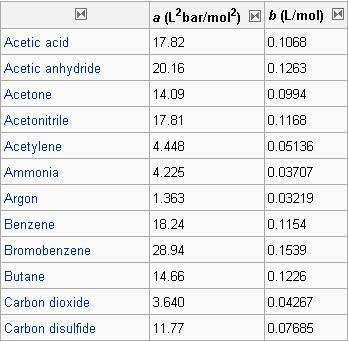
I coefficienti a e b sono specifici per la specie chimica gassosa presa in considerazione ed in considerazione della loro importanza sono noti e tabulati per tutte le più importanti sostanze allo stato gassoso. Più questi coefficienti risultano distanti dal valore di zero, più il gas considerato può essere considerato intrinsecamente distante da un gas ideale.