Indice
Avete tra le mani un prodotto liquido per uso domestico e sulla confezione c’è scritto di dosarne un certo numero di millilitri (ml) o di centimetri cubi (cm3 o c.c.) e non avete idea di come si faccia.
DIGRESSIONE SU PESO SPECIFICO E DENSITA’
Perché dovremmo parlare di densità e non di peso specifico? Dietro a questa semplice domanda si aprirebbe a dire il vero una piccola-grande diatriba che i divulgatori della fisica si trascinano dietro da anni… per dirla in due parole: quello che noi abitualmente siamo soliti chiamare il “peso” di un oggetto o di una sostanza, in realtà non dovrebbe essere chiamato peso bensì massa, fermo restando tutte le unità di misura alle quali siamo abituati, ovvero grammi, chilogrammi, tonnellate, ecc. Quello che i fisici chiamano scientificamente come “peso” sarebbe in realtà una forza, la forza con la quale l’oggetto è richiamato verso terra (o, se volete, con la quale esso preme sul piatto di una bilancia), grazie a quella che comunemente di indica come “forza di gravità” e che in realtà, dal punto di vista fisico, dovrebbe essere chiamata “accelerazione” di gravità terrestre. Non per niente si apprende fra le prime nozioni di fisica che una forza che agisce su un corpo è data dal prodotto della sua massa per l’accelerazione che agisce su di essa.
Da qui il fatto, noto a molti di noi almeno come nozione appresa, che andando sulla luna, su un altro pianeta o comunque molto molto lontano dalla terra (ovunque la gravità, ovvero “l’accelerazione di gravità” sia minore) lo stesso oggetto peserebbe molto di meno. Peserebbe di meno anche se appoggiato sul piatto di una bilancia. Seppur su scala molto ridotta, questo effetto lo si potrebbe registrare, sempre restando sul nostro pianeta, semplicemente passando dal livello del mare alla montagna d’alta quota.
Quindi il peso non è un indice assoluto per misurare la quantità di una data sostanza perché risente dell’entità dell’accelerazione di gravità. Un valore sicuramente più assoluto è invece quello della massa che, specie per materiali complessi come sono le miscele di sostanze chimiche, non ultimi gli stessi ingredienti alimentari, può essere considerata un ottimo modo per misurare la quantità del materiale trattato.
Quello che a livello popolare viene quindi definito come “peso specifico” dovrebbe quindi a maggior rigore essere definito come “massa specifica”, se vogliamo che diventi una caratteristica intrinseca del materiale considerato. La massa specifica è più brevemente indicata come “densità”.
Ma qui il fraintendimento sta ancora in agguato nei termini. Un po’ tutti abbiamo ben fissata nella mente l’immagine di un liquido “denso” come un liquido che fatica a scorrere, sciropposo, oleoso, molto viscoso… Ecco: per questo genere di materiali il termine “denso” è usato a sproposito e dovrebbe essere sostituito con l’aggettivo “viscoso”. L’olio è certamente più viscoso, ma meno denso dell’acqua, ed è per questo che galleggia sopra ad essa. Il concetto di densità può essere applicato ovviamente anche a materiali non liquidi, come ad esempio gas o solidi: l’acciaio è più denso dell’acqua ed è per questo che dadi e bulloni di acciaio non galleggiano ma stanno a fondo in un bicchiere d’acqua.
A livello più microscopico, mentre la viscosità è motivata dall’inerzia con la quale le molecole si oppongono ai loro spostamenti reciproci indotti dall’esterno, in pratica allo “scivolamento” di una molecola sull’altra che si verifica durante il trasferimento o il mescolamento del liquido, la densità dipende invece da quanto le molecole risultano fra loro compattate, con la capacità di riempire più o meno bene un certo volume con un numero più o meno grande di molecole. Essendo ovviamente le molecole, con i loro atomi, e non lo spazio vuoto fra una molecola e l’altra, a determinare la massa di un corpo, anche di un liquido, più le molecole risultano “addensate” fra loro, più la densità del materiale risulterà elevata.
Quindi la densità dovrebbe essere correttamente “immaginata” come la quantità di materia, o anche la quantità di massa, che sta racchiusa in un volume unitario (es. 1 litro) di sostanza. In termini microscopici, una specie chimica le cui molecole restano ben impaccate l’una vicina all’altra, minimizzando gli spazi vuoti, risulterà essere più “concentrata” dello stesso volume e pertanto avrà densità più elevata.
Quindi, riassumendo, avevamo inizialmente a che fare con ben 3 diverse confusioni lessicali: massa/peso, da questa peso specifico / densità, ed infine densità/viscosità. Spero che dopo questa breve spiegazione i principali dubbi siano stati dissolti e si possa iniziare ad utilizzare in modo appropriato la grandezza della densità, almeno per quanto riguarda il caso in vero un po’ semplificato rappresentato dai liquidi. Fatta questa digressione, dal momento che non è comunemente possibile, almeno a livello domestico, effettuare con una bilancia o con altra strumentazione una misura della massa svincolata dall’accelerazione di gravità e che quest’ultima può essere intesa come sufficientemente costante nell’ambito della superficie terrestre, accetteremo il compromesso verbale di utilizzare, come da consuetudine, la parola “peso” dove a rigore dovrebbe essere utilizzato il termine “massa”
In un prossimo post introdurremo invece concetti più appropriati per la misura della densità dei materiali solidi (dalle polveri ai granuli, fino ad oggetti interi), particolarmente utile ad esempio per il riconoscimento della natura dei medesimi e per la valutazione delle loro caratteristiche, come ad esempio la differenza fra densità apparente e la densità assoluta e gli strumenti, anche di natura domestica, utilizzabili per la misura di questi valori.
LA GRADUAZIONE DEL MISURINO
Torniamo ora al problema pratico della graduazione del nostro contenitore.
Se riuscissimo a trovare una sostanza particolare, un caso davvero speciale, la cui densità fosse esattamente uguale ad 1, significherebbe che un millilitro di questa peserebbe esattamente un grammo, ovvero un litro peserebbe un chilo, ovvero ancora un metro cubo (1000 litri) peserebbe una tonnellata. Guardiamoci un po’ intorno alla ricerca di questa specie di stele di Rosetta dei liquidi… E’ l’acqua!!!
In realtà non si tratta di un caso: per ovvie ragioni di abbondanza e di importanza la densità dell’acqua è servita in passato come riferimento per esprimere la densità di tutti gli altri materiali.
In particolare il riferimento pari esattamente ad 1 g/ml è quello relativo all’acqua pura alla temperatura di +4°C alla pressione di 1 bar, ovvero al livello del mare.
Pertanto per il caso speciale dell’acqua, essendo la densità pari ad 1, il valore numerico del peso in grammi “solo per questa sostanza” sarà esattamente uguale al volume in millilitri. Ad esempio 23 ml di acqua pesano esattamente 23 grammi, ed ovviamente viceversa. Quindi se vogliamo graduare il nostro misurino a 47 millilitri, è sufficiente che lo mettiamo sul piatto della bilancia, azzeriamo la tara ed aggiungiamo gradualmente acqua fino al raggiungimento del peso di 47 g. A questo punto appoggiamo il misurino sul piano del tavolo, mettiamoci con lo sguardo a livello dell’intefaccia liquido-aria (praticamente mettiamoci allo stesso livello di altezza del liquido) e segniamo con il pennarello la linea che corrisponde al livello dell’acqua: 47 g, “ovvero” (solo per l’acqua) 47 ml.
Parlare di centimetri cubi o cc è del tutto equivalente a parlare di millilitri (ml), come d’altronde un decimetro cubo (ovvero un volume corrispondente ad un cubo di 10x10x10 cm) corrisponde a quello che siamo abituati a chiamare litro.
Ovviamente il misurino non ci servirà nel futuro per misurare l’acqua ma un liquido differente che avrà quasi certamente densità diversa, maggiore o minore, rispetto a quella dell’acqua. Ma a questo punto nessun problema: se per l’acqua la graduazione che abbiamo tracciato poteva misurare indifferentemente il volume o l’equivalente in peso, per le altre sostanza con densità diverse da uno, la stessa tacchetta continuerà a misurare un volume corretto, ma semplicemente esso non sarà più numericamente equivalente al peso del liquido.
Possiamo fare molte tacchette sullo stesso contenitore, riferite a volumi diversi di acqua.
Se il contenitore è perfettamente cilindrico, senza restringimenti o allargamenti, ovvero di sezione costante, possiamo per esempio segnare una tacchetta in corrispondenza di un volume molto piccolo (es. 10 ml, corrispondenti a 10 g di acqua) ed una in corrispondenza di un volume molto grande (es. 100 ml): con righello e pennarello possiamo quindi dividere la distanza fra queste due tacchette in un numero uguale di tacche più piccole: ad esempio la differenza 100 ml – 10 ml = 90 ml può agevolmente essere divisa in 9 tacche uguali. Se la distanza sulla bottiglietta fra le due tacche è, facciamo un’ipotesi, di 13 cm, 13 cm diviso 9 fa circa 1.4 cm, ovvero 14 mm. Sarà per tanto possibile riportare un tacchetta ogni 14 mm che rappresenterà la graduazione di 10 ml.
Possiamo anche utilizzare contenitori che alla base o in cima non hanno forma cilindrica, magari per via di uno svasamento o di un collo, purché la graduazione venga effettuata solo nella zona cilindrica del contenitore.
Se invece non fossimo riusciti a procurarci un misurino in alcun modo cilindrico, per effettuare graduazioni intermedie dovremmo ripetere numerose volte la pesata di quantità diverse di acqua, togliendo ogni volta che abbiamo pesato il contenitore dalla bilancia, appoggiandolo sul piano e segnando il nuovo livello raggiunto dall’acqua, con insieme il valore numerico letto sulla bilancia.
Il noto contenitore di forma conica usato nei laboratori chimici ma anche in alcune case, la beuta o matraccio di Erlenmeyer, riporta di solito stampata sulla sua superficie una graduazione che è solo un’indicazione approssimata del suo volume: la principale complicazione è rappresentata in questo caso dall’inclinazione delle pareti che fa sì, come è possibile notare in figura, che le tacche di graduazione non siano distanziate in modo costante l’una dall’altra, ma si avvicinino fra loro al crescere del diametro della sezione del contenitore.
Solo un’ultima raccomandazione relativa alla temperatura: come ci insegna il principio di funzionamento dei vecchi termometri a mercurio, o se volete anche quelli ad alcol… comunque dei classici termometri “a colonnina”, il cui zona colorata (costituita da un liquido) “si alza”, ovvero sale di livello, in relazione alla temperatura dell’ambiente, il volume del liquido è dipendente dalla temperatura.
“Solitamente” il volume cresce al crescere della temperatura anche se non tutti i liquidi rispondono nello stesso modo alla medesima variazione della temperatura.
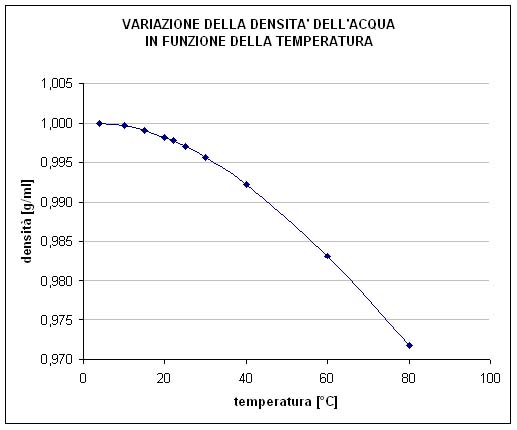
Pertanto se abbiamo graduato il nostro misurino in una calda giornata estiva e poi pensiamo di utilizzarlo in un gelido inverno per dosare un liquido in ambiente esterno, e siamo così sfortunati da avere a che fare con un liquido caratterizzato da un elevato “coefficiente di dilatazione termica” (il valore che indica di quanto si dilata il volume per ogni grado di aumento della temperatura), la graduazione effettuata potrebbe risultare di fatto un po’ sfalsata rispetto alla realtà. Anche la stessa acqua varia il suo volume, a parità di peso, in funzione della temperatura: nella figura qui a fianco si può vedere come essa passi da 1 g/ml esatto alla temperatura di +4°C (al livello del mare) a 0.9718 g/ml ad 80°C. Da un esame superficiale dei numeri il valore della sua densità non sembra essere cambiato di molto, eppure tale variazione corrisponde ad un “errore” (nel caso in cui utilizzassimo lo stesso misurino per le due temperature) di quasi il 3%. Per altri liquidi, come ad esempio quelli a base alcolica e per molti combustibili, questo errore sarebbe decisamente maggiore.
E SE VOLESSIMO SVINCOLARCI DALLA TEMPERATURA?
In questo caso, se volessimo effettuare delle misure sia più precise che più accurate ad ogni temperatura di lavoro, il mio suggerimento è quello di iniziare a ragionare in termini di peso (ehm… di “massa”), anziché di volume. Questo per due diverse ragioni, entrambe altrettanto valide: la prima è di natura scientifica ed è relativa all’invarianza del peso in relazione alla temperatura: se preleviamo da un flacone10 g di un antiparassitario da diluire e li mettiamo in un bicchierino, questi peseranno sempre 10 g indipendentemente dalla temperatura e persino dalla pressione alla quale saranno esposti (ovviamente a meno che una parte del prodotto evapori). La seconda ragione è di natura pratica: tanto in laboratorio quanto e soprattutto in casa, sono molto più affidabili gli strumenti in grado di misurare il peso (le bilance) piuttosto che quelli in grado di misurare il volume (contenitori graduati, pipette, contagocce, matracci, pompe, misuratori elettronici di varia natura, ecc).
Il problema è che, a differenza dell’acqua, gli altri liquidi hanno una densità solitamente diversa da 1 e di solito non conosciuta a priori. Come possiamo allora trasformare la dose di liquido richiesta in volume nella corrispondente dose in peso, invariante con la temperatura?
Niente di più facile: prendiamo il contenitore che abbiamo appena graduato e misuriamone la tara su un bilancino sensibile da cucina, uno di quelli in grado di misurare i singoli grammi, meglio se addirittura i decimi di grammo. Quindi riempiamolo fino ad una certa tacca con il liquido da valutare, ad esempio fino alla tacca che segna i 25 ml. Misuriamo il peso sulla bilancia di questi 25 ml netti di liquido (es. 30 g).
Dividendo il peso (in grammi) per il volume (in ml o cc) otteniamo la densità, espressa in g/ml o se preferite in g/cc, riferita a quello specifico liquido ed alla temperatura della misura, possibilmente quella ambientale (circa 20°C).
Densità = peso [g] / volume [ml] = 30 g / 25 ml = 1.2 g/ml
Immagino che chi ha compilato le istruzioni e le dosi di impiego di un prodotto liquido, se non si è espresso diversamente, intendesse riferirsi a condizioni volumetriche misurabili a temperatura ambiente.
Per ottenere il peso in grammi corrispondente alla quantità in volume indicata dal produttore (es. 80 ml), si moltiplica il volume richiesto per la densità appena calcolata per quel dato liquido:
Peso [g] = volume [ml] x densità [g/ml] = 80 ml x 1.2 g/ml = 96 g
Quindi 96 g del liquido in questione, tanto in una fredda giornata invernale quanto in una torrida estiva, saranno equivalenti alla quantità di prodotto che, riportata a temperatura ambiente, corrisponderà ad un volume di 80 ml (o 80 cc) dello stesso liquido.